题目内容
(请注意求和符号:f(k)+f(k+1)+f(k+2)+…+f(n)=| n |
 |
| i=k |
已知常数a为正实数,曲线Cn:y=
| nx |
(1)求证:点列:P1,P2,…,Pn在同一直线上
(2)求证:ln(n+1)<
| n |
 |
| i=1 |
| ||
| yi |
| n |
分析:(1)欲求出切线方程,只须求出其斜率即可,故先利用导数求出在x=xn处的导函数值,再结合导数的几何意义即可求出切线的斜率.Pn(a,
)总在直线x=a上,即P1,P2,,Pn在同一直线上,从而问题解决.
(2)由(1)可知yn=
,从而f(i)=
=
=
,对
=
进行放缩
从而得出:
=
<
2(
-
)=2[(
-
)+(
-
)++(
-
)]=2
,最后设函数F(x)=
-ln(x+1),x∈[0,1],利用导数研究其单调性即可证得结论.
| na |
(2)由(1)可知yn=
| an |
| ||
| yi |
| 1 | ||
|
|
| 1 | ||
|
| 2 | ||
2
|
| 2 | ||||
|
| n |
 |
| i=1 |
| ||
| yi |
| n |
 |
| i=1 |
| 1 | ||
|
| n |
 |
| i=1 |
| i |
| i-1 |
| 1 |
| 0 |
| 2 |
| 1 |
| n |
| n-1 |
| n |
| x |
解答:证:(1)∵f(x)=
,
∴f′(x)=
•(nx)′=
•
.(1分)
Cn:y=
在点Pn(xn,yn)处的切线ln的斜率kn=f′(xn)=
•
,
∴ln的方程为y-yn=
•
(x-xn).(2分)
∵ln经过点(-a,0),
∴yn=-
•
(-a-xn)=
•
(a+xn).
又∵Pn在曲线Cn上,∴yn=
=
•
(a+xn),
∴xn=a,∴yn=
,∴Pn(a,
)总在直线x=a上,
即P1,P2,,Pn在同一直线x=a上.(4分)
(2)由(1)可知yn=
,∴f(i)=
=
=
.(5分)
=
<
=2(
-
)(i=1,2,,n),
=
<
2(
-
)
=2[(
-
)+(
-
)++(
-
)]=2
.(9分)
设函数F(x)=
-ln(x+1),x∈[0,1],有F(0)=0,
∴F′(x)=
-
=
=
>0(x∈(0,1)),
∴F(x)在[0,1]上为增函数,
即当0<x<1时F(x)>F(0)=0,故当0<x<1时
>ln(x+1)恒成立.(11分)
取x=
(i=1,2,3,,n),f(i)=
>ln(1+
)=ln(i+1)-lni,
即f(1)=
>ln2,f(2)=
>ln(1+
)=ln3-ln2,,f(n)=
>ln(n+1)-lnn,
∴
f(i)=
=
+
+
>ln2+(ln3-ln2)++[ln(n+1)-lnn]=ln(n+1)
综上所述有ln(n+1)<
<2
(n∈N*).(13分).
| nx |
∴f′(x)=
| 1 | ||
2
|
| 1 |
| 2 |
|
Cn:y=
| nx |
| 1 |
| 2 |
|
∴ln的方程为y-yn=
| 1 |
| 2 |
|
∵ln经过点(-a,0),
∴yn=-
| 1 |
| 2 |
|
| 1 |
| 2 |
|
又∵Pn在曲线Cn上,∴yn=
| nxn |
| 1 |
| 2 |
|
∴xn=a,∴yn=
| na |
| na |
即P1,P2,,Pn在同一直线x=a上.(4分)
(2)由(1)可知yn=
| an |
| ||
| yi |
| 1 | ||
|
|
| 1 | ||
|
| 2 | ||
2
|
| 2 | ||||
|
| i |
| i-1 |
| n |
 |
| i=1 |
| ||
| yi |
| n |
 |
| i=1 |
| 1 | ||
|
| n |
 |
| i=1 |
| i |
| i-1 |
=2[(
| 1 |
| 0 |
| 2 |
| 1 |
| n |
| n-1 |
| n |
设函数F(x)=
| x |
∴F′(x)=
| 1 | ||
2
|
| 1 |
| x+1 |
x+1-2
| ||
2
|
(
| ||
2
|
∴F(x)在[0,1]上为增函数,
即当0<x<1时F(x)>F(0)=0,故当0<x<1时
| x |
取x=
| 1 |
| i |
|
| 1 |
| i |
即f(1)=
| 1 | |
|
|
| 1 |
| 2 |
|
∴
| n |
 |
| i=1 |
| n |
 |
| i=1 |
|
|
|
|
综上所述有ln(n+1)<
| n |
 |
| i=1 |
| ||
| yi |
| n |
点评:本小题主要考查函数单调性的应用、利用导数研究曲线上某点切线方程、不等式的证明等基础知识,考查运算求解能力、化归与转化思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
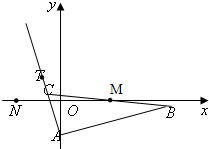 已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足
已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足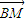 =
=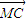 ,点T(-1,1)在AC边所在直线上且满足
,点T(-1,1)在AC边所在直线上且满足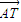 =
=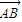 .
.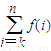 ,其中k,n为正整数且k≤n.
,其中k,n为正整数且k≤n.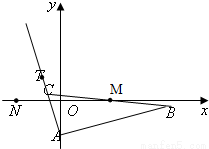
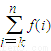 ,其中k,n为正整数且k≤n)
,其中k,n为正整数且k≤n)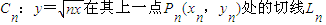 总经过定点(-a,0)(n∈N*)
总经过定点(-a,0)(n∈N*)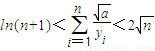 (n∈N*)
(n∈N*)