题目内容
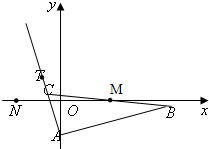 已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足
已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足| BM |
| MC |
| AT |
| AB |
(I)求AC边所在直线的方程;
(II)求△ABC外接圆的方程;
(III)若动圆P过点N(-2,0),且与△ABC的外接圆外切,求动圆P的圆心的轨迹方程.
请注意下面两题用到求和符号:
f(k)+f(k+1)+f(k+2)+…+f(n)=
| n |
 |
| i=k |
分析:(I)由
•
=0,T在AC上,知△ABC是直角三角形.由AB边所在的直线方程是x-3y-6=0,知直线AC的斜率是-3,再由T(-1,1)在直线AC上,能求出AC边所在的直线方程.
(II)AC与AB的交点为A,由
,解得A(0,-2).由
=
,知M(2,0)为Rt△ABC外接圆的圆心,再由r=|AM|=
=2
,能求出△ABC外接圆的方程.
(III)由动圆P过点N,知|PN|是该圆的半径,再由动圆P与圆M外切,知|PM|=|PN|+2
,由此能得到点P的轨迹.
| AT |
| AB |
(II)AC与AB的交点为A,由
|
| BM |
| MC |
| (2-0)2+(0+2)2 |
| 2 |
(III)由动圆P过点N,知|PN|是该圆的半径,再由动圆P与圆M外切,知|PM|=|PN|+2
| 2 |
解答:解:(I)∵
•
=0,∴AT⊥AB,
∵T在AC上,∴AC⊥AB,△ABC是直角三角形.
又AB边所在的直线方程是x-3y-6=0,
∴直线AC的斜率是-3,
∵T(-1,1)在直线AC上,
∴AC边所在的直线方程是y-1=-3(x+1),即3x+y+2=0.
(II)AC与AB的交点为A,
由
,解得A(0,-2).
∵
=
,
∴M(2,0)为Rt△ABC外接圆的圆心,
∵r=|AM|=
=2
,
∴△ABC外接圆的方程为:(x-2)2+y2=8.
(III)∵动圆P过点N,所以|PN|是该圆的半径,
又∵动圆P与圆M外切,
∴|PM|=|PN|+2
,即|PM|-|PN|=2
.
故点P的轨迹是以M,N为焦点,实轴长为2
的双曲线的左支.
| AT |
| AB |
∵T在AC上,∴AC⊥AB,△ABC是直角三角形.
又AB边所在的直线方程是x-3y-6=0,
∴直线AC的斜率是-3,
∵T(-1,1)在直线AC上,
∴AC边所在的直线方程是y-1=-3(x+1),即3x+y+2=0.
(II)AC与AB的交点为A,
由
|
∵
| BM |
| MC |
∴M(2,0)为Rt△ABC外接圆的圆心,
∵r=|AM|=
| (2-0)2+(0+2)2 |
| 2 |
∴△ABC外接圆的方程为:(x-2)2+y2=8.
(III)∵动圆P过点N,所以|PN|是该圆的半径,
又∵动圆P与圆M外切,
∴|PM|=|PN|+2
| 2 |
| 2 |
故点P的轨迹是以M,N为焦点,实轴长为2
| 2 |
点评:本题考查圆的性质和应用,解题时要认真审题,注意直线和圆的位置关系的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
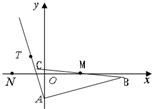 已知△ABC的边AB所在直线的方程为x-3y-6=0,M(2,0)满足
已知△ABC的边AB所在直线的方程为x-3y-6=0,M(2,0)满足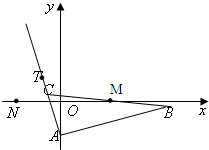 已知△ABC的边AB边所在直线的方程为x-3y-6=0点B关于点M(2,0)的对称点为C,点T(-1,1)在AC边所在直线上且满足
已知△ABC的边AB边所在直线的方程为x-3y-6=0点B关于点M(2,0)的对称点为C,点T(-1,1)在AC边所在直线上且满足 (2012•东莞二模)已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足
(2012•东莞二模)已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足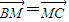 ,点T(-1,1)在AC边所在直线上且满足
,点T(-1,1)在AC边所在直线上且满足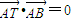 .
.