题目内容
定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有 <0,则( )
<0,则( )
A.f(3)<f(-2)<f(1) B.f(1)<f(-2)<f(3)
C.f(-2)<f(1)<f(3) D.f(3)<f(1)<f(-2)
【答案】
A
【解析】
试题分析:因为对任意的x1,x2∈[0,+∞)(x1≠x2),有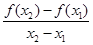 <0,所以f(x)在[0,+∞)上是单调递减,所以f(3)<f(2)<f(1),又因为f(x)是偶函数,f(-2)= f(2),所以f(3)<f(-2)<f(1)。
<0,所以f(x)在[0,+∞)上是单调递减,所以f(3)<f(2)<f(1),又因为f(x)是偶函数,f(-2)= f(2),所以f(3)<f(-2)<f(1)。
考点:本题考查偶函数的定义、性质和单调函数的性质。
点评:函数的奇偶性和单调性是非常重要的两条性质,在学习的过程中,我们一定要掌握熟练。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知定义在R上的偶函数f(x).当x≥0时,
已知定义在R上的偶函数f(x).当x≥0时,