题目内容
已知函数y1=x+ (x≠0),y2=cosx+
(x≠0),y2=cosx+ (0<x<
(0<x< ),y3=
),y3= (x>0),y4=(1+cotx)(
(x>0),y4=(1+cotx)( +tanx)(0<x<
+tanx)(0<x< ),其中以4为最小值的函数个数是( )
),其中以4为最小值的函数个数是( )A.0
B.1
C.2
D.3
【答案】分析:通过举特例,可得y1不满足条件. 利用基本不等式可得y2=4的条件是cosx=2,这不可能,故y2不满足条件.
利用基本不等式可得y3的最大值是4,故y3不满足条件.利用基本不等式可得y4的最小值为 ,故y4不满足条件.
,故y4不满足条件.
解答:解:当x<0时, <0,故y1不满足条件.
<0,故y1不满足条件.
当0<x< 时,cosx∈(0,1),
时,cosx∈(0,1), ≥4,当且仅当
≥4,当且仅当 即cosx=2时,等号成立.
即cosx=2时,等号成立.
由于cosx=2 不可能,故y2的最小值大于4,故y2不满足条件.
当x>0时, =
= ≤4,当且仅当 x=1时,等号成立.故4是y3的最大值,故y3不满足条件.
≤4,当且仅当 x=1时,等号成立.故4是y3的最大值,故y3不满足条件.
当0<x< 时,tanx>0,cotx>0,
时,tanx>0,cotx>0, =
= +2tanx+
+2tanx+ cotx≥
cotx≥ =
= ,
,
故y4的最小值为 .故y4不满足条件.
.故y4不满足条件.
故选:A.
点评:本题主要考查三角函数的最值,基本不等中等号式成立的条件,属于中档题.
利用基本不等式可得y3的最大值是4,故y3不满足条件.利用基本不等式可得y4的最小值为
 ,故y4不满足条件.
,故y4不满足条件.解答:解:当x<0时,
 <0,故y1不满足条件.
<0,故y1不满足条件.当0<x<
 时,cosx∈(0,1),
时,cosx∈(0,1), ≥4,当且仅当
≥4,当且仅当 即cosx=2时,等号成立.
即cosx=2时,等号成立.由于cosx=2 不可能,故y2的最小值大于4,故y2不满足条件.
当x>0时,
 =
= ≤4,当且仅当 x=1时,等号成立.故4是y3的最大值,故y3不满足条件.
≤4,当且仅当 x=1时,等号成立.故4是y3的最大值,故y3不满足条件.当0<x<
 时,tanx>0,cotx>0,
时,tanx>0,cotx>0, =
= +2tanx+
+2tanx+ cotx≥
cotx≥ =
= ,
,故y4的最小值为
 .故y4不满足条件.
.故y4不满足条件.故选:A.
点评:本题主要考查三角函数的最值,基本不等中等号式成立的条件,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
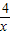 (x≠0),y2=cosx+
(x≠0),y2=cosx+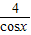 (0<x<
(0<x<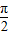 ),y3=
),y3=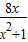 (x>0),y4=(1+cotx)(
(x>0),y4=(1+cotx)( +tanx)(0<x<
+tanx)(0<x<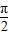 ),其中以4为最小值的函数个数是( )
),其中以4为最小值的函数个数是( )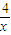 (x≠0),y2=cosx+
(x≠0),y2=cosx+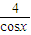 (0<x<
(0<x<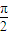 ),y3=
),y3=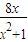 (x>0),y4=(1+cotx)(
(x>0),y4=(1+cotx)( +tanx)(0<x<
+tanx)(0<x<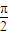 ),其中以4为最小值的函数个数是( )
),其中以4为最小值的函数个数是( )