题目内容
已知函数y1=x+
(x≠0),y2=cosx+
(0<x<
),y3=
(x>0),y4=(1+cotx)(
+tanx)(0<x<
),其中以4为最小值的函数个数是( )
| 4 |
| x |
| 4 |
| cosx |
| π |
| 2 |
| 8x |
| x2+1 |
| 1 |
| 2 |
| π |
| 2 |
分析:通过举特例,可得y1不满足条件. 利用基本不等式可得y2=4的条件是cosx=2,这不可能,故y2不满足条件.
利用基本不等式可得y3的最大值是4,故y3不满足条件.利用基本不等式可得y4的最小值为
,故y4不满足条件.
利用基本不等式可得y3的最大值是4,故y3不满足条件.利用基本不等式可得y4的最小值为
| 9 |
| 2 |
解答:解:当x<0时,y1=x+
<0,故y1不满足条件.
当0<x<
时,cosx∈(0,1),y2=cosx+
≥4,当且仅当cosx=
即cosx=2时,等号成立.
由于cosx=2 不可能,故y2的最小值大于4,故y2不满足条件.
当x>0时,y3=
=
≤4,当且仅当 x=1时,等号成立.故4是y3的最大值,故y3不满足条件.
当0<x<
时,tanx>0,cotx>0,y4=( 1+cotx ) (
+2tanx )=
+2tanx+
cotx≥
+2=
,
故y4的最小值为
.故y4不满足条件.
故选:A.
| 4 |
| x |
当0<x<
| π |
| 2 |
| 4 |
| cosx |
| 4 |
| cosx |
由于cosx=2 不可能,故y2的最小值大于4,故y2不满足条件.
当x>0时,y3=
| 8x |
| x2+1 |
| 8 | ||
x+
|
当0<x<
| π |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 9 |
| 2 |
故y4的最小值为
| 9 |
| 2 |
故选:A.
点评:本题主要考查三角函数的最值,基本不等中等号式成立的条件,属于中档题.

练习册系列答案
相关题目
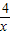 (x≠0),y2=cosx+
(x≠0),y2=cosx+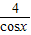 (0<x<
(0<x<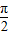 ),y3=
),y3=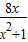 (x>0),y4=(1+cotx)(
(x>0),y4=(1+cotx)( +tanx)(0<x<
+tanx)(0<x<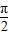 ),其中以4为最小值的函数个数是( )
),其中以4为最小值的函数个数是( ) (x≠0),y2=cosx+
(x≠0),y2=cosx+ (0<x<
(0<x< ),y3=
),y3= (x>0),y4=(1+cotx)(
(x>0),y4=(1+cotx)( +tanx)(0<x<
+tanx)(0<x< ),其中以4为最小值的函数个数是( )
),其中以4为最小值的函数个数是( )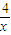 (x≠0),y2=cosx+
(x≠0),y2=cosx+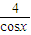 (0<x<
(0<x<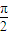 ),y3=
),y3=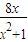 (x>0),y4=(1+cotx)(
(x>0),y4=(1+cotx)( +tanx)(0<x<
+tanx)(0<x<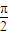 ),其中以4为最小值的函数个数是( )
),其中以4为最小值的函数个数是( )