题目内容
(2011•重庆模拟)在半径为1的球内有一内接正四棱柱,正四棱柱的高为
,一个动点从正四棱柱的一个顶点出发沿球面运动到达另一个顶点,则经过的最短路程是( )
| 2 |
分析:由题意,设内接正四棱柱的底面边长为a,利用内接正四棱柱的对角线长即为球的直径,求出a=1,如图,在三角形OAB中,OA=OB=AB=1,求出A,B间的球面距离即得所求答案,由图及题意可知球心角∠AOB,再由弧长公式求出四段弧长,即可求得答案
解答: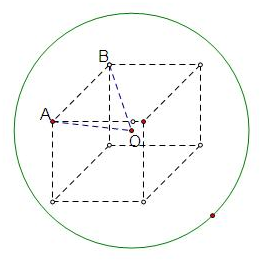 解:由题意,设内接正四棱柱的底面边长为a,则
解:由题意,设内接正四棱柱的底面边长为a,则
内接正四棱柱的对角线长即为球的直径,即:
2a2+(
) 2=2 2⇒a=1,如图,在三角形OAB中,OA=OB=AB=1,
∴球心角∠AOB=
经过的最短路程是:
×1=
故选D.
 解:由题意,设内接正四棱柱的底面边长为a,则
解:由题意,设内接正四棱柱的底面边长为a,则内接正四棱柱的对角线长即为球的直径,即:
2a2+(
| 2 |
∴球心角∠AOB=
| π |
| 3 |
经过的最短路程是:
| π |
| 3 |
| π |
| 3 |
故选D.
点评:本题考查多面体与旋转体表面上的最短距离,弧长公式,考查了空间想像能力及由图形进行计算的能力,考查了数形结合的思想.

练习册系列答案
相关题目
 (2011•重庆模拟)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式为( )
(2011•重庆模拟)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式为( )