题目内容
【题目】设函数![]() ,则下列结论错误的是( )
,则下列结论错误的是( )
A. f(x)的一个周期为-2π
B. y=f(x)的图象关于直线x=![]() 对称
对称
C. f(x+π)的一个零点为x=![]()
D. f(x)在![]() 单调递减
单调递减
【答案】D
【解析】对于A选项,因为f(x)=cos![]() 的周期为2kπ(k∈Z),所以f(x)的一个周期为-2π,A项正确.对于B选项,因为f(x)=cos
的周期为2kπ(k∈Z),所以f(x)的一个周期为-2π,A项正确.对于B选项,因为f(x)=cos![]() 图象的对称轴为直线x=kπ-
图象的对称轴为直线x=kπ-![]() (k∈Z),所以y=f(x)的图象关于直线x=
(k∈Z),所以y=f(x)的图象关于直线x=![]() 对称,B项正确.对于C选项,f(x+π)=cos
对称,B项正确.对于C选项,f(x+π)=cos![]() .令x+
.令x+![]() =kπ+
=kπ+![]() (k∈Z),得x=kπ-
(k∈Z),得x=kπ-![]() ,当k=1时,x=
,当k=1时,x=![]() ,所以f(x+π)的一个零点为x=
,所以f(x+π)的一个零点为x=![]() ,C项正确.对于D选项,因为f(x)=cos
,C项正确.对于D选项,因为f(x)=cos![]() 的递减区间为(2kπ-
的递减区间为(2kπ-![]() ,2kπ+
,2kπ+![]() ) (k∈Z),递增区间为(2kπ+
) (k∈Z),递增区间为(2kπ+![]() ,2kπ+
,2kπ+![]() )(k∈Z),所以
)(k∈Z),所以![]() 是减区间,(
是减区间,(![]() ,π)是增区间,D项错误.故选D.
,π)是增区间,D项错误.故选D.

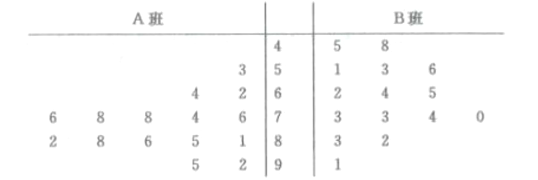
【题目】在创建“全国文明卫生城”过程中,某市“创城办”为了调查市民对创城工作的了解情况,进行了一次创城知识问卷调查(一位市民只能参加一次).通过随机抽样,得到参加问卷调查的1000人的得分(满分100分)统计结果如下表所示.
组别 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由频数分布表可以大致认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
, ![]() 近似为这1000人得分的平均值值(同一组数据用该组数据区间的中点值表示),请用正态分布的知识求
近似为这1000人得分的平均值值(同一组数据用该组数据区间的中点值表示),请用正态分布的知识求![]() ;
;
(2)在(1)的条件下,“创城办”为此次参加问卷调查的市民制定如下奖励方案::
(ⅰ)得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
(ⅱ)每次获赠送的随机话费和对应的概率为:
赠送的随机话费(单元:元) | 20 | 40 |
概率 | 0.75 | 0.25 |
现有市民甲要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:参考数据与公式
![]() ,若
,若![]() ,则
,则
①![]() ;
;
②![]() ;
;
③![]() .
.