题目内容
圆心在直线y=x上的圆M经过点(2,0),且在x轴上截得的弦长为4,则圆M的标准方程为 (只要求写出一个即可).
【答案】分析:设出圆的方程,利用圆经过(2,0)与在x轴上的截距为4,列出方程组,即可求出圆的方程.
解答:解:由于圆心在y=x上,所以可设圆的方程为(x-a)2+(y-a)2=r2,将y=0代入得:x2-2ax+2a2=r2
∴x1+x2=a,x1•x2=2a2-r2,
∴弦长=|x1-x2 |=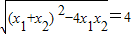 ,
,
代入可得:7a2-4r2+16=0 ①
再将点(2,0)代入方程(x-a)2+(y-a)2=r2,
得2a2-2a+4-r2=0…②,
联立①②即可解出a=0、r=2,或a=8,r2=116
于是方程为:x2+y2=4或(x-8)2+(y-8)2=116.
故答案为:x2+y2=4或(x-8)2+(y-8)2=116.
点评:本题考查圆的标准方程的求法,弦长的求法,考查计算能力.
解答:解:由于圆心在y=x上,所以可设圆的方程为(x-a)2+(y-a)2=r2,将y=0代入得:x2-2ax+2a2=r2
∴x1+x2=a,x1•x2=2a2-r2,
∴弦长=|x1-x2 |=
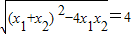 ,
,代入可得:7a2-4r2+16=0 ①
再将点(2,0)代入方程(x-a)2+(y-a)2=r2,
得2a2-2a+4-r2=0…②,
联立①②即可解出a=0、r=2,或a=8,r2=116
于是方程为:x2+y2=4或(x-8)2+(y-8)2=116.
故答案为:x2+y2=4或(x-8)2+(y-8)2=116.
点评:本题考查圆的标准方程的求法,弦长的求法,考查计算能力.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目