题目内容
已知函数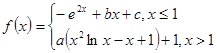 函数
函数 在
在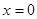 处取得极值1.
处取得极值1.
(1)求实数b,c的值;
(2)求 在区间[-2,2]上的最大值.
在区间[-2,2]上的最大值.
(1)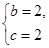 (2)详见解析.
(2)详见解析.
解析试题分析:(1)根据分段函数可知,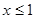 时,
时,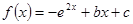 ,根据函数
,根据函数 在
在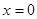 处,取得极值1,可知
处,取得极值1,可知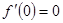 ,
,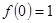 ,求出
,求出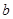 与
与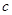 ,并且回代函数,验证能够满足在
,并且回代函数,验证能够满足在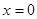 处函数取得极值;
处函数取得极值;
(2)当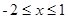 时,函数
时,函数 ,
,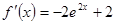 ,求函数的极值点,与端点值,判定最大值,当
,求函数的极值点,与端点值,判定最大值,当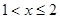 时,
时,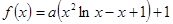 ,
,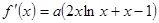 ,设
,设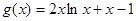 ,显然大于0,所以只要讨论
,显然大于0,所以只要讨论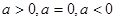 三种情况的正负,取得函数的单调性,闭区间内求最大值,再与
三种情况的正负,取得函数的单调性,闭区间内求最大值,再与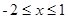 的最大值比较大小.
的最大值比较大小.
(1)由题意当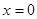 时,
时, ,
,
当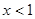 时,
时, 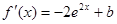 ,
,
依题意得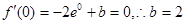 ,
,
经检验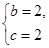 符合条件. 4分
符合条件. 4分
(2)由(1)知,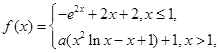
当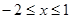 时,
时,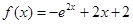 ,
,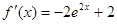 ,
,
令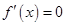 得
得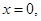
当 变化时,
变化时,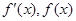 的变化情况如下表:
的变化情况如下表:
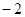
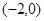
0 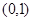
1 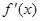
+ 0 — 
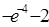
 练习册系列答案
练习册系列答案
剑指中考系列答案
名师点睛教材详解系列答案
课堂精练解读与指导系列答案
初中语文阅读专题训练系列答案
本土好学生小升初系统总复习系列答案
周自主读本系列答案
初中学业考试总复习系列答案
综合素质测评卷系列答案
新课标中学区域地理系列答案
四清导航早读手册系列答案
相关题目
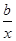 ,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.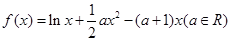 .
.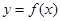 在点(1,f(1))处的切线方程;
在点(1,f(1))处的切线方程;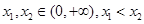 ,且
,且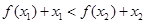 恒成立,求a的取值范围.
恒成立,求a的取值范围.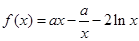 .
. 在
在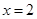 时有极值,求实数
时有极值,求实数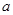 的值和
的值和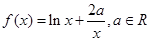 .
. 在
在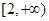 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;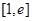 上的最小值为3,求实数
上的最小值为3,求实数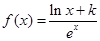 (其中
(其中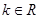 ),
),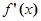 为f(x)的导函数.
为f(x)的导函数.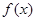 在点(1,
在点(1,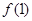 )处的切线不过点(2,0);
)处的切线不过点(2,0);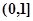 中存在
中存在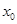 ,使得
,使得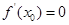 ,求
,求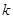 的取值范围;
的取值范围;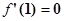 ,试证明:对任意
,试证明:对任意 ,
,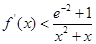 恒成立.
恒成立.
 为自然对数的底数).
为自然对数的底数). 在
在 处的切线方程;
处的切线方程; 是
是 的一个极值点,且点
的一个极值点,且点 ,
, 满足条件:
满足条件: .
.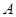 ,
, ,
, 是三个不同的点,且构成直角三角形.
是三个不同的点,且构成直角三角形.