题目内容
已知向量 ,
,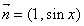 ,
,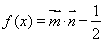 .
.
(1)求函数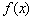 的单调递减区间;
的单调递减区间;
(2)在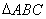 中,
中,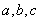 分别是角
分别是角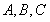 的对边,
的对边,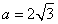 ,
,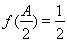 ,
,
若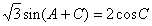 ,求
,求 的大小.
的大小.
【答案】
(1)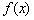 递减区间是
递减区间是 . (2)
. (2)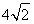 .
.
【解析】
试题分析:(1)利用平面向量的坐标运算及三角函数公式,将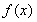 化简为
化简为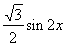 ,确定得到
,确定得到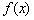 递减区间.
递减区间.
(2)由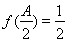 和
和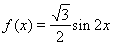 求得
求得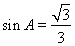 ,利用三角函数同角公式得
,利用三角函数同角公式得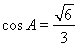 或
或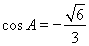 .
.
注意讨论两种情况只有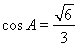 ,求得
,求得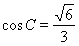 ,再求
,再求 ,应用正弦定理得解.
,应用正弦定理得解.
试题解析:(1)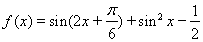
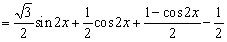
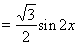 4分
4分
所以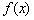 递减区间是
递减区间是 . 5分
. 5分
(2)由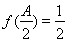 和
和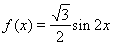 得:
得: 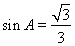 6分
6分
若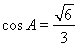 ,而
,而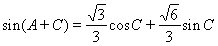
又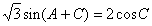 ,所以
,所以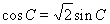
因为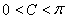 ,所以
,所以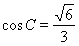
若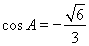 ,同理可得:
,同理可得: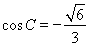 ,显然不符合题意,舍去. 9分
,显然不符合题意,舍去. 9分
所以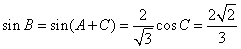 10分
10分
由正弦定理得: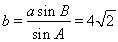 12分
12分
考点:平面向量的数量积,三角函数同角公式,两角和的三角函数,正弦余弦定理的应用,三角形面积公式.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目