题目内容
下列几个命题:其中正确的有________.(以序号作答)
①函数y=4cos2x,x∈[-l0π,10π]不是周期函数;
②“m=-2”是“直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的充分不必要条件;
③函数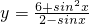 的最小值为
的最小值为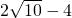 .
.
④已知m2+n2=4,x2+y2=9,则mx+ny的最大值为 ;
;
①②
分析:根据周期的定义判断①;两条直线垂直关系判断②;函数的最值的求法判断③;三角代换求最值判断④,推出正确结论.
解答:①函数y=4cos2x,x∈[-l0π,10π]不是周期函数,正确;
②“m=-2”是“直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的充分不必要条件;正确,因为m=2时两条直线也垂直.
③函数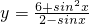 的最小值为
的最小值为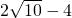 .因为
.因为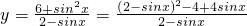 ≥
≥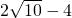 的解答是不正确的,不满足等号成立的条件,所以不正确.
的解答是不正确的,不满足等号成立的条件,所以不正确.
④已知m2+n2=4,x2+y2=9,则mx+ny的最大值为 ;利用三角代换,求出mx+ny的最大值为
;利用三角代换,求出mx+ny的最大值为 ,所以不正确.
,所以不正确.
故答案为:①②
点评:本题考查两条直线垂直的判定,函数的最值及其几何意义,基本不等式,考查逻辑思维能力,计算能力,是基础题.
分析:根据周期的定义判断①;两条直线垂直关系判断②;函数的最值的求法判断③;三角代换求最值判断④,推出正确结论.
解答:①函数y=4cos2x,x∈[-l0π,10π]不是周期函数,正确;
②“m=-2”是“直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的充分不必要条件;正确,因为m=2时两条直线也垂直.
③函数
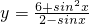 的最小值为
的最小值为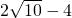 .因为
.因为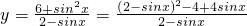 ≥
≥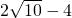 的解答是不正确的,不满足等号成立的条件,所以不正确.
的解答是不正确的,不满足等号成立的条件,所以不正确.④已知m2+n2=4,x2+y2=9,则mx+ny的最大值为
 ;利用三角代换,求出mx+ny的最大值为
;利用三角代换,求出mx+ny的最大值为 ,所以不正确.
,所以不正确.故答案为:①②
点评:本题考查两条直线垂直的判定,函数的最值及其几何意义,基本不等式,考查逻辑思维能力,计算能力,是基础题.

练习册系列答案
相关题目