题目内容
(本题满分14分)离心率为![]() 的椭圆
的椭圆![]() 上有一点
上有一点![]() 到椭圆两焦点的距离和为
到椭圆两焦点的距离和为![]() .以椭圆
.以椭圆![]() 的右焦点
的右焦点![]() 为圆心,短轴长为直径的圆有切线
为圆心,短轴长为直径的圆有切线![]() (
(![]() 为切点),且点
为切点),且点![]() 满足
满足![]() (
(![]() 为椭圆
为椭圆![]() 的上顶点)。(I)求椭圆的方程;(II)求点
的上顶点)。(I)求椭圆的方程;(II)求点![]() 所在的直线方程
所在的直线方程![]() .
.
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
解析:
:(I)依题意有: 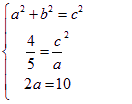 3分解得:
3分解得: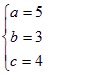 5分
5分
所以椭圆方程为:![]() 。6分
。6分
(II)设点![]() 。由(I)得
。由(I)得![]() ,所以圆
,所以圆![]() 的方程为:
的方程为:![]() .……8分
.……8分
方法一(根轴法):把![]() 点当作圆
点当作圆![]() :
:![]() ,点
,点![]() 所在的直线是圆
所在的直线是圆![]() 和圆
和圆![]() 的根轴,所以
的根轴,所以![]() ,即
,即![]() 。
。
方法二(圆幂定理):![]() ,……10分
,……10分
![]() ,
,![]() ,12分
,12分
所以![]() ,……13分化简得:
,……13分化简得:![]() 。………14分
。………14分
方法三(勾股定理):![]() 为直角三角形,所以
为直角三角形,所以 ![]() 。又
。又![]() ,所以
,所以![]() ,化简得:
,化简得:![]() .
.

练习册系列答案
相关题目
 ,长轴长为
,长轴长为 ,离心率
,离心率 ,过右焦点
,过右焦点 的直线
的直线 交
交 ,
, 两点:
两点: 的面积;
的面积;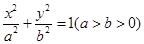 的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足
的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足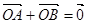 (
(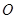 是坐标原点),
是坐标原点),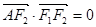 ,若椭圆的离心率等于
,若椭圆的离心率等于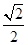 .
. 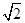 ,求椭圆的方程;
,求椭圆的方程;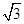 .
.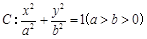 的左焦点
的左焦点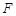 及点
及点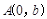 ,原点
,原点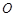 到直线
到直线 的距离为
的距离为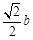 .
.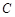 的离心率
的离心率 ;
;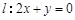 的对称点
的对称点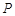 在圆
在圆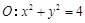 上,求椭圆
上,求椭圆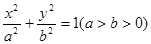 的离心率为
的离心率为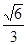 ,长轴长为
,长轴长为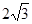 ,直线
,直线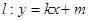 交椭圆于不同的两点A、B。
交椭圆于不同的两点A、B。 的值(O点为坐标原点);
的值(O点为坐标原点);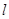 的距离为
的距离为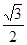 ,求
,求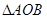 面积的最大值。
面积的最大值。