题目内容
某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为 米,圆心角为
米,圆心角为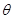 (弧度).
(弧度).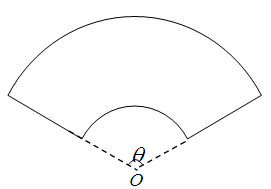
(1)求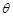 关于
关于 的函数关系式;
的函数关系式;
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为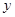 ,求
,求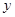 关于
关于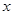 的函数关系式,并求出
的函数关系式,并求出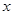 为何值时,
为何值时,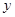 取得最大值?
取得最大值?
(1)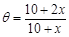 (2)
(2)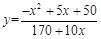 ,
,
解析试题分析:(1) 解决应用题问题首先要解决阅读问题,具体说就是要会用数学式子正确表示数量关系,本题解题思路清晰,就是根据扇环面的周长列函数关系式,因为扇环面的周长为两段弧长加两段直线,利用弧长公式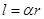 ,得
,得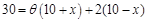 所以
所以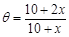 ,(2) 本题解题思路清晰,就是根据花坛的面积与装饰总费用的比列函数关系式,再由导数或基本不等式求最值. 装饰总费用为直线部分的装饰费用与弧线部分的装饰费用之和,而花坛的面积为大扇形面积与小扇形面积之差,求最值时要注意定义域范围的限制.
,(2) 本题解题思路清晰,就是根据花坛的面积与装饰总费用的比列函数关系式,再由导数或基本不等式求最值. 装饰总费用为直线部分的装饰费用与弧线部分的装饰费用之和,而花坛的面积为大扇形面积与小扇形面积之差,求最值时要注意定义域范围的限制.
试题解析:(1)设扇环的圆心角为q,则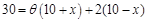 ,所以
,所以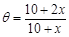 , 4分
, 4分
(2) 花坛的面积为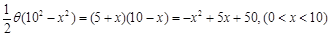 . 7分
. 7分
装饰总费用为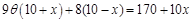 , 9分
, 9分
所以花坛的面积与装饰总费用的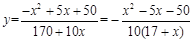 , 12分
, 12分
令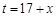 ,则
,则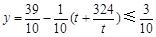 ,当且仅当t=18时取等号,此时
,当且仅当t=18时取等号,此时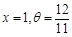 .
.
答:当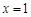 时,花坛的面积与装饰总费用的比最大. 15分
时,花坛的面积与装饰总费用的比最大. 15分
考点:函数关系式,弧长公式,基本不等式求最值

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

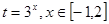 ,求
,求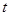 的最大值与最小值;
的最大值与最小值;  的最大值与最小值;
的最大值与最小值; 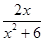 .
.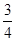 是省外游客,其余是省内游客.在省外游客中有
是省外游客,其余是省内游客.在省外游客中有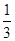 持金卡,在省内游客中有
持金卡,在省内游客中有 持银卡.(1)在该团中随机采访2名游客,求恰有1人持银卡的概率;
持银卡.(1)在该团中随机采访2名游客,求恰有1人持银卡的概率; 表示,且
表示,且 (其中
(其中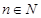 ),又知建5座球场时,每平方米的平均建筑费用为400元.
),又知建5座球场时,每平方米的平均建筑费用为400元.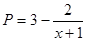 (其中
(其中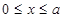 ,a为正常数);已知生产该产品还需投入成本(10+2P)万元(不含促销费用),产品的销售价格定为
,a为正常数);已知生产该产品还需投入成本(10+2P)万元(不含促销费用),产品的销售价格定为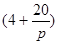 万元/万件.
万元/万件.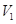 .
.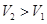 吗?若能、给出你的一种设计方案。
吗?若能、给出你的一种设计方案。  .
.