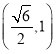题目内容
【题目】已知函数![]() .
.
(1)求![]() 的定义域;
的定义域;
(2)判断![]() 的奇偶性;
的奇偶性;
(3)求使![]() 的x的取值范围.
的x的取值范围.
【答案】(1)(﹣1,1)(2)见解析(3)![]()
【解析】
(1)根据使函数解析式有意义的原则,可构造关于x的不等式组,求出f(x)的定义域;
(2)由(1)中函数的定义域为(﹣1,1),再由f(﹣x)=ln(1﹣x)﹣ln(1+x)=﹣f(x),可知此函数为奇函数.
(3)根据对数函数的单调性,将不等式转化为分式不等式,进而再转化为整式不等式,可得满足条件的x的取值范围.
解:(1)若使函数解析式有意义,自变量x须满足:
x+1>0,且1﹣x>0,
解得:﹣1<x<1,
故f(x)的定义域为(﹣1,1)
(2)由(1)中函数的定义域(﹣1,1)关于原点对称,
又由f(﹣x)=ln(1﹣x)﹣ln(1+x)=﹣f(x),
故f(x)为奇函数
(3)∵f(x)=ln(x+1)﹣ln(1﹣x)![]() ,
,
若f(x)>0,即![]() ,
,
∴![]()
∴![]() ,
,
∴![]()
∴![]() 的x的取值范围
的x的取值范围![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某校为了推动数学教学方法的改革,学校将高一年级部分生源情况基本相同的学生分成甲、乙两个班,每班各![]() 人,甲班按原有模式教学,乙班实施教学方法改革,经过一年的教学,将甲、乙两个班学生一年来的数学成绩取整数,绘制成如下茎叶图,规定不低于
人,甲班按原有模式教学,乙班实施教学方法改革,经过一年的教学,将甲、乙两个班学生一年来的数学成绩取整数,绘制成如下茎叶图,规定不低于![]() 分(百分制)为优秀,甲班同学成绩的中位数为
分(百分制)为优秀,甲班同学成绩的中位数为![]() .
.

(1)求![]() 的值和乙班同学成绩的众数;
的值和乙班同学成绩的众数;
(2)完成表格,若有![]() 以上的把握认为“数学成绩优秀与教学改革有关”的话,那么学校将扩大教学改革面,请问学校是否要扩大教学改革面?说明理由.
以上的把握认为“数学成绩优秀与教学改革有关”的话,那么学校将扩大教学改革面,请问学校是否要扩大教学改革面?说明理由.
甲班 | 乙班 | 合计 | |
优秀人数 | |||
不优秀人数 | |||
合计 |
附:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 | |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |