题目内容
【题目】已知函数![]() ,若函数
,若函数![]() 在
在![]() 上存在两个极值点
上存在两个极值点![]() .
.
(Ⅰ)求实数![]() 的取值范围;
的取值范围;
(Ⅱ)证明:![]() .
.
【答案】(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】
(Ⅰ)求出![]() ,分析
,分析![]() 的符号,
的符号,![]() 的根的个数满足的条件.
的根的个数满足的条件.
(Ⅱ)不妨设![]() ,令
,令![]() ,
,![]() ,将目标不等式的参数减少,用分析的方法最后证明:
,将目标不等式的参数减少,用分析的方法最后证明:![]() ,构造函数证明即可.
,构造函数证明即可.
(Ⅰ)函数![]() 的定义域为
的定义域为![]() ,
,
因为![]() ,
,
![]()
令![]()
所以![]() .
.
当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递增.
上单调递增.
即![]() 在
在![]() 上单调递增,
上单调递增,
![]() 在
在![]() 上至多一个零点,
上至多一个零点,
所以![]() 在
在![]() 上至多一个极值点,不满足条件.
上至多一个极值点,不满足条件.
当![]() 时,由
时,由![]() ,得
,得![]() (负根舍去),
(负根舍去),
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() )上单调递减;
)上单调递减;
在![]() 上单调递增.
上单调递增.
所以![]() ,
,
要使函数![]() 在
在![]() 上存在两个极值点
上存在两个极值点
则函数![]() 有两个零点,即
有两个零点,即![]() 有两个零点
有两个零点
首先![]() ,解得
,解得![]() .
.
因为![]() ,且
,且![]() ,
,
下面证明:![]() .
.
设![]() ,
,
则![]() .
.
因为![]() ,所以
,所以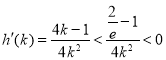 .
.
所以![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() .
.
所以实数![]() 的取值范围为
的取值范围为![]() .
.
(Ⅱ)因为![]() ,
,![]() 是函数
是函数![]() 的两个极值点,
的两个极值点,
所以![]() ,
,![]() 是函数
是函数![]() 的两个零点
的两个零点
即![]() ,
,![]() 是函数
是函数![]() 的两个零点,
的两个零点,
不妨设![]() ,令
,令![]() ,则
,则![]() .
.
所以 即
即![]() .
.
所以![]() ,即
,即![]() ,
,![]() ,
,![]() .
.
要证![]() ,需证
,需证![]() .
.
即证![]() ,即证
,即证![]() .
.
因为![]() ,所以即证
,所以即证![]() .
.
设![]() ,
,
则![]() .
.
所以![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() .
.
所以![]() .
.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案【题目】在贯彻中共中央、国务院关于精准扶贫政策的过程中,某单位在某市定点帮扶甲、乙两村各50户贫困户为了做到精准帮扶,工作组对这100户村民的年收入情况、劳动能力情况、子女受教育情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标x,将指标x按照![]() 分成五组,得到如图所示的频率分布直方图.
分成五组,得到如图所示的频率分布直方图.

规定若![]() ,则认定该户为“绝对贫困户”,否则认定该户为“相对贫困户”,且当
,则认定该户为“绝对贫困户”,否则认定该户为“相对贫困户”,且当![]() 时,认定该户为“低收入户”;当
时,认定该户为“低收入户”;当![]() 时,认定该户为“亟待帮助户”,已知此次调查中甲村的“绝对贫困户”占甲村贫困户的24%.
时,认定该户为“亟待帮助户”,已知此次调查中甲村的“绝对贫困户”占甲村贫困户的24%.
(1)完成下面的列联表,并判断是否有90%的把握认为绝对贫困户数与村落有关;
甲村 | 乙村 | 总计 | |
绝对贫困户 | |||
相对贫困户 | |||
总计 |
(2)若两村“低收入户”中乙村“低收入户”占比为![]() ,两村“亟待帮助户”中乙村“亟待帮助户”占比为
,两村“亟待帮助户”中乙村“亟待帮助户”占比为![]() ,且乙村贫困指标在
,且乙村贫困指标在![]() 上的户数成等差数列,试估计乙村贫困指标x的平均值
上的户数成等差数列,试估计乙村贫困指标x的平均值![]() .
.
附: ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |


