题目内容
设x,y满足约束条件
|
| x+2y+3 |
| x+1 |
| 3 |
| 2 |
分析:先根据约束条件画出可行域,再利用几何意义求最值,z=
中的
表示过点(x,y)与(-1.-1)连线的斜率,只需求出可行域内的点与(-1,-1)连线的斜率即可.
| x+2y+3 |
| x+1 |
| y+1 |
| x+1 |
解答: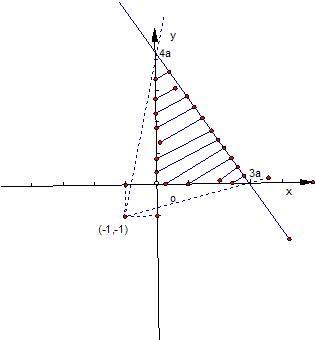 解:∵
解:∵
=1+2×
,
而
表示过点(x,y)与(-1.-1)连线的斜率,
易知a>0,所以可作出可行域,
知
的最小值是
,
即(
)min=
=
=
?a=1.
故填:1.
 解:∵
解:∵| x+2y+3 |
| x+1 |
| y+1 |
| x+1 |
而
| y+1 |
| x+1 |
易知a>0,所以可作出可行域,
知
| y+1 |
| x+1 |
| 1 |
| 4 |
即(
| y+1 |
| x+1 |
| 0-(-1) |
| 3a-(-1) |
| 1 |
| 3a+1 |
| 1 |
| 4 |
故填:1.
点评:涉及到线性规划的题目,每年必考;就此题而言,式子z=
的处理应当成为解决本题的关键,一般来说,高考题中的分式结构在处理方式上一般是分离变形,这样其几何意义就表现来了.本题主要考查了简单的线性规划,以及利用几何意义求最值,属于基础题.
| x+2y+3 |
| x+1 |

练习册系列答案
相关题目