题目内容
(2011•奉贤区二模)(文)设x,y满足约束条件
若z=
的最小值为
,则a的值
|
| y+1 |
| x+1 |
| 1 |
| 4 |
1
1
.分析:先根据约束条件画出可行域,再利用z的几何意义求最值,只需求出何时可行域内的点与点(-1,-1)连线的斜率的值最小,从而得到 a的值.
解答: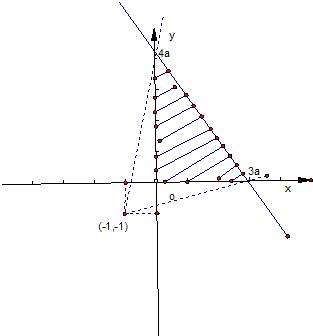 解:先根据约束条件画出可行域,
解:先根据约束条件画出可行域,
因为z的值就是可行域内的点与点(-1,-1)连线的斜率的值,
当点在可行域内的(3a,0)时,z=
有最小值为
,
即z=
=
=
,解得:a=1.
故答案为:1.
 解:先根据约束条件画出可行域,
解:先根据约束条件画出可行域,因为z的值就是可行域内的点与点(-1,-1)连线的斜率的值,
当点在可行域内的(3a,0)时,z=
| y+1 |
| x+1 |
| 1 |
| 4 |
即z=
| y+1 |
| x+1 |
| 0+1 |
| 3a+1 |
| 1 |
| 4 |
故答案为:1.
点评:本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011•奉贤区二模)(文) 如图都是由边长为1的正方体叠成的图形.例如第(1)个图形的表面积为6个平方单位,第(2)个图形的表面积为18个平方单位,第(3)个图形的表面积是36个平方单位.依此规律,则第n个图形的表面积是
(2011•奉贤区二模)(文) 如图都是由边长为1的正方体叠成的图形.例如第(1)个图形的表面积为6个平方单位,第(2)个图形的表面积为18个平方单位,第(3)个图形的表面积是36个平方单位.依此规律,则第n个图形的表面积是 (2011•奉贤区二模)用2π平方米的材料制成一个有盖的圆锥形容器,如果在制作过程中材料无损耗,且材料的厚度忽略不计,底面半径长为x,圆锥母线的长为y
(2011•奉贤区二模)用2π平方米的材料制成一个有盖的圆锥形容器,如果在制作过程中材料无损耗,且材料的厚度忽略不计,底面半径长为x,圆锥母线的长为y