题目内容
已知函数f（x）=2|x+1|+|x-2|．
（Ⅰ）请写出函数f（x）在每段区间上的解析式，并在图中的直角坐标系中作出函数f（x）的图象；
（Ⅱ）若不等式f（x）≥a2-2a对任意的实数x恒成立，求实数a的取值范围．
（Ⅰ）请写出函数f（x）在每段区间上的解析式，并在图中的直角坐标系中作出函数f（x）的图象；
（Ⅱ）若不等式f（x）≥a2-2a对任意的实数x恒成立，求实数a的取值范围．
分析：（Ⅰ）化简函数f（x）=2|x+1|+|x-2|的解析式为
，画出图象．
（Ⅱ）对?x∈R，f（x）≥a2-2a恒成立，而函数f（x）的最小值为3，故有3≥a2-2a恒成立，由此求得实数a的取值范围．
|
（Ⅱ）对?x∈R，f（x）≥a2-2a恒成立，而函数f（x）的最小值为3，故有3≥a2-2a恒成立，由此求得实数a的取值范围．
解答：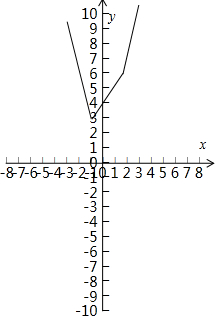
解：（Ⅰ）函数f（x）=2|x+1|+|x-2|=
，直角坐标系中如图所示：
（Ⅱ）对?x∈R，f（x）≥a2-2a恒成立，而函数f（x）的最小值为3，3≥a2-2a恒成立，即a2-2a-3≤0，
解得-1≤a≤3，
故实数a的取值范围为[-1，3]．
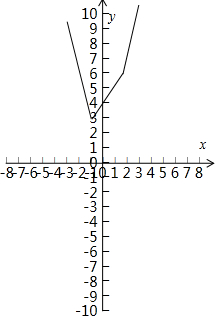解：（Ⅰ）函数f（x）=2|x+1|+|x-2|=
|
（Ⅱ）对?x∈R，f（x）≥a2-2a恒成立，而函数f（x）的最小值为3，3≥a2-2a恒成立，即a2-2a-3≤0，
解得-1≤a≤3，
故实数a的取值范围为[-1，3]．
点评：本题主要考查带有绝对值的函数，函数的恒成立问题，一元二次不等式的解法，属于中档题．
练习册系列答案
智能训练练测考系列答案
相关题目