题目内容
1.△ABC中三边上的高依次为$\frac{1}{13},\frac{1}{5},\frac{1}{11}$,则△ABC为( )| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 不存在这样的三角形 |
分析 利用已知条件结合三角形的面积推出三边关系,然后利用余弦定理判断求解即可.
解答 解:设△ABC三边分别为a,b,c,${S_{△ABC}}=\frac{1}{2}a•\frac{1}{13}=\frac{1}{2}b•\frac{1}{11}=\frac{1}{2}c•\frac{1}{5}$,
所以$\frac{a}{13}=\frac{b}{11}=\frac{c}{5}$,
设a=13k,b=11k,c=5k(k>0).
因为11k+5k>13k,故能构成三角形,取大角A,
$cosA=\frac{{{b^2}+{c^2}-{a^2}}}{2bc}=\frac{{{{11}^2}+{5^2}-{{13}^2}}}{2×11×5}<0$,
所以A为钝角,
所以△ABC为钝角三角形.
点评 本题是完全原创;原创的理由:①对三角形形状的判断,利用到面积公式、余弦定理等知识进行解决;②考查考生分析问题的能力.

练习册系列答案
相关题目
18.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),F1,F2是其左、右焦点,点P为双曲线的右支上一点,点M为圆心,圆M为三角形PF1F2的内切圆,PM所在直线与x轴的交点坐标为(1,0),与双曲线的一条渐近线平行且距离为$\frac{\sqrt{2}}{2}$,则双曲线C的离心率是( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
3.已知sinx-cosx=$\frac{1}{5}$(0≤x<π),则tanx等于( )
| A. | -$\frac{3}{4}$ | B. | -$\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
6.下列赋值语句正确的是( )
| A. | a+b=5 | B. | 5=a | C. | a+b=c | D. | a=a+1 |
13.已知点F1、F2分别是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左、右焦点,过F1且垂直于x轴的直线与椭圆交于 M、N两点,若△M NF2为等腰直角三角形,则该椭圆的离心率e为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $-1+\sqrt{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
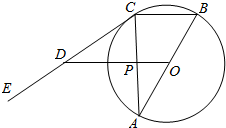 如图,已知AB是圆O的直径,AB=4,EC是圆O的切线,切点为C,BC=1,过圆心O做BC的平行线,分别交EC和AC于点D和点P,求OD.
如图,已知AB是圆O的直径,AB=4,EC是圆O的切线,切点为C,BC=1,过圆心O做BC的平行线,分别交EC和AC于点D和点P,求OD.