题目内容
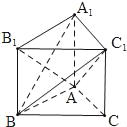
【题目】已知三棱柱ABC﹣A1B1C1中，AA1⊥面ABC，AB⊥AC，且AA1=AB=AC，则异面直线AB1与BC1所成角为_____．
【答案】
【解析】连结A1B，
∵AA1⊥面ABC，平面A1B1C1∥面ABC，
∴AA1⊥平面A1B1C1，
∵A1C1平面A1B1C1，∴AA1⊥A1C1，
∵△ABC与△A1B1C1是全等三角形，AB⊥AC，
∴A1B1⊥A1C1，
∵A1B1∩AA1=A1，∴A1C1⊥平面AA1B1B，
又∵AB1平面AA1B1B，∴A1C1⊥AB1，
∵矩形AA1B1B中，AA1=AB，
∴四边形AA1B1B为正方形，可得A1B⊥AB1，
∵A1B∩A1C1=A1，∴AB1⊥平面A1BC1，
结合BC1平面A1BC1，可得AB1⊥BC1，即异面直线AB1与BC1所成角为
．
故答案为
．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
【题目】小萌大学毕业后，家里给了她10万元，她想办一个“萌萌”加工厂，根据市场调研，她得出了一组毛利润
（单位：万元）与投入成本
（单位：万元）的数据如下：
投入成本 | 0.5 | 1 | 2 | 3 | 4 | 5 | 6 |
毛利润 | 1.06 | 1.25 | 2 | 3.25 | 5 | 7.25 | 9.98 |
为了预测不同投入成本情况下的利润，她想在两个模型
，
中选一个进行预测.
（1）根据投入成本2万元和4万元的两组数据分别求出两个模型的函数解析式，请你根据给定数据选出一个较好的函数模型进行预测（不必说明理由），并预测她投入8万元时的毛利润；
（2）若小萌准备最少投入2万元开办加工厂，请预测加工厂毛利润率
的最大值，并说明理由.（
）
