题目内容
设![]() ,等差数列
,等差数列![]() 中
中![]() ,
,![]() ,记
,记![]() =
=![]() ,令
,令![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() .
.
(Ⅰ)求![]() 的通项公式和
的通项公式和![]() ;
;
(Ⅱ)求证:![]() ;
;
(Ⅲ)是否存在正整数![]() ,且
,且![]() ,使得
,使得![]() 成等比数列?若存在,求出
成等比数列?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
(Ⅰ)![]() Sn=
Sn=![]() =
=![]()
(Ⅱ)见解析
(Ⅲ)![]() 成等比数列,存在正整数m=2,n=16,且1<m<n,使得
成等比数列,存在正整数m=2,n=16,且1<m<n,使得![]() 成等比数列
成等比数列
解析:
(Ⅰ)设数列![]() 的公差为
的公差为![]() ,由
,由![]() ,
,![]() .
.
解得![]() ,
,![]() =3 ∴
=3 ∴![]()
∵![]() ∴Sn=
∴Sn=![]() =
=![]() .
.
(Ⅱ) ![]()
∴![]() ∴
∴![]()
(Ⅲ)由(2)知,![]() ∴
∴![]() ,
,![]()
∵![]() 成等比数列.
成等比数列.
∴ ![]() 即
即![]()
当![]() 时,7
时,7![]() ,
,![]() =1,不合题意;
=1,不合题意;
当![]() 时,
时,![]()
![]() ,
,![]() =16,符合题意;
=16,符合题意;
当![]() 时,
时,![]()
![]() ,
,![]() 无正整数解;
无正整数解;
当![]() 时,
时,![]()
![]() ,
,![]() 无正整数解;
无正整数解;
当![]() 时,
时,![]()
![]() ,
,![]() 无正整数解;
无正整数解;
当![]() 时,
时,![]()
![]() ,
,![]() 无正整数解;
无正整数解;
当![]() 时,
时,![]() ,则
,则![]() ,而
,而![]() ,
,
所以,此时不存在正整数m,n,且1<m<n,使得![]() 成等比数列.
成等比数列.
综上,存在正整数m=2,n=16,且1<m<n,使得![]() 成等比数列.
成等比数列.

练习册系列答案
相关题目
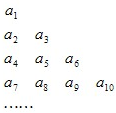 将数列{an}中的所有项按每一行比上一行多一项的规则排成如数表:
将数列{an}中的所有项按每一行比上一行多一项的规则排成如数表: