题目内容
已知中心在坐标原点、焦点在x轴上椭圆的离心率 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+2相切.
,以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+2相切.(1)求该椭圆的标准方程;
(2)设椭圆的左,右焦点分别是F1和F2,直线l1过F2且与x轴垂直,动直线l2与y轴垂直,l2交l1于点P,求线段PF1的垂直平分线与l2的交点M的轨迹方程,并指明曲线类型.
【答案】分析:(1)设出椭圆的方程,利用椭圆的离心率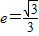 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+2相切,可求椭圆的几何量,从而可得椭圆的标准方程;
,以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+2相切,可求椭圆的几何量,从而可得椭圆的标准方程;
(2)利用线段PF1的垂直平分线与l2的交点为M,可得|MF1|=|MP|,由此可得M的轨迹方程及曲线类型.
解答:解:(1)依题意设所求椭圆方程为
∵椭圆的离心率 ,
,
∴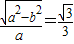 ,∴2a2=3b2①
,∴2a2=3b2①
又以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+2相切.
即原点到直线y=x+2的距离为b,所以 ,代入①中得
,代入①中得
所以,所求椭圆方程为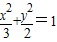 .…(6分)
.…(6分)
(2)由 得F1、F2点的坐标分别为(-1,0),(1,0),
得F1、F2点的坐标分别为(-1,0),(1,0),
设M点的坐标为(x,y),由题意:P点坐标为(1,y),
因为线段PF1的垂直平分线与l2的交点为M,
所以|MF1|=|MP|,∴ ,∴y2=-4x
,∴y2=-4x
故线段PF1的垂直平分线与l2的交点M的轨迹方程是y2=-4x,
该轨迹是以F1为焦点的抛物线.…(12分)
点评:本题考查椭圆的标准方程,考查直线与圆的位置关系,考查轨迹方程,考查学生的计算能力,属于中档题.
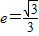 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+2相切,可求椭圆的几何量,从而可得椭圆的标准方程;
,以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+2相切,可求椭圆的几何量,从而可得椭圆的标准方程;(2)利用线段PF1的垂直平分线与l2的交点为M,可得|MF1|=|MP|,由此可得M的轨迹方程及曲线类型.
解答:解:(1)依题意设所求椭圆方程为

∵椭圆的离心率
 ,
,∴
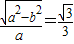 ,∴2a2=3b2①
,∴2a2=3b2①又以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+2相切.
即原点到直线y=x+2的距离为b,所以
 ,代入①中得
,代入①中得
所以,所求椭圆方程为
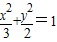 .…(6分)
.…(6分)(2)由
 得F1、F2点的坐标分别为(-1,0),(1,0),
得F1、F2点的坐标分别为(-1,0),(1,0),设M点的坐标为(x,y),由题意:P点坐标为(1,y),
因为线段PF1的垂直平分线与l2的交点为M,
所以|MF1|=|MP|,∴
 ,∴y2=-4x
,∴y2=-4x故线段PF1的垂直平分线与l2的交点M的轨迹方程是y2=-4x,
该轨迹是以F1为焦点的抛物线.…(12分)
点评:本题考查椭圆的标准方程,考查直线与圆的位置关系,考查轨迹方程,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 (2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率
(2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率