题目内容
已知离心率为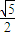 的双曲线C的中心在坐标原点,左、右焦点F1、F2在x轴上,双曲线C的右支上一点A使
的双曲线C的中心在坐标原点,左、右焦点F1、F2在x轴上,双曲线C的右支上一点A使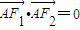 且△F1AF2的面积为1.
且△F1AF2的面积为1.(1)求双曲线C的标准方程;
(2)若直线l:y=kx+m与双曲线C相交于E、F两点(E、F不是左右顶点),且以EF为直径的圆过双曲线C的右顶点D.求证:直线l过定点,并求出该定点的坐标.
【答案】分析:(1)由题意设双曲线的标准方程为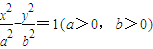 ,由已知得:
,由已知得: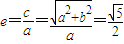 ,解得a=2b.由
,解得a=2b.由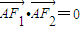 且△F1AF2的面积为1,知(|F1A|-|F2A|)2=4c2-4=4a2,由此能求出双曲线C的方程.
且△F1AF2的面积为1,知(|F1A|-|F2A|)2=4c2-4=4a2,由此能求出双曲线C的方程.
(2)△=(8km)2-4(4m2+4)(4k2-1)>0,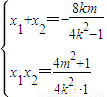 ,
,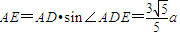 ,由以EF为直径的圆过双曲线C的右顶点D(2,0),知Rt△PAE即
,由以EF为直径的圆过双曲线C的右顶点D(2,0),知Rt△PAE即 ,由此入手能够导出直线过定点(
,由此入手能够导出直线过定点(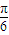 ,0).
,0).
解答:解:(1)由题意设双曲线的标准方程为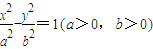 ,
,
由已知得: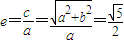 解得a=2b,
解得a=2b,
∵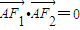 且△F1AF2的面积为1,
且△F1AF2的面积为1,
∴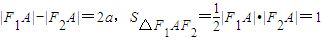 ,,|F1A|2+|F2A|2=|F1F2|2
,,|F1A|2+|F2A|2=|F1F2|2
∴(|F1A|-|F2A|)2=4c2-4=4a2
∴b=1,a=2,
∴双曲线C的保准方程为 .
.
(2)设E(x1,y1),F(x2,y2) 联立y=kx+m与双曲线
-y2=1
得(4k2-1)x2+8kmx+4(m2+1)=0
△=(8km)2-4(4m2+4)(4k2-1)>0
即4k2-m2-1<0
则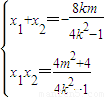 ,
,
又∴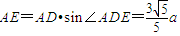
∵以EF为直径的圆过双曲线C的右顶点D(2,0)
∴Rt△PAE即
∴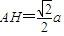
∴ ,且均满足
,且均满足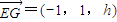 .
.
∵AC1⊥EG,∴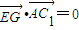 .
.
当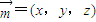 时,直线
时,直线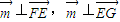 的方程为
的方程为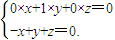 ,
,
直线过定点(2,0),与已知矛盾!
当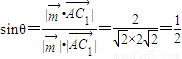 时,
时,
直线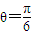 的方程为θ,直线过定点(
的方程为θ,直线过定点(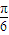 ,0)
,0)
∴直线l定点,定点坐标为( ,0).
,0).
点评:本题考查双曲线的方程的求法和求证直线l过定点,并求出该定点的坐标.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
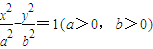 ,由已知得:
,由已知得: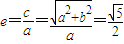 ,解得a=2b.由
,解得a=2b.由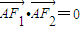 且△F1AF2的面积为1,知(|F1A|-|F2A|)2=4c2-4=4a2,由此能求出双曲线C的方程.
且△F1AF2的面积为1,知(|F1A|-|F2A|)2=4c2-4=4a2,由此能求出双曲线C的方程.(2)△=(8km)2-4(4m2+4)(4k2-1)>0,
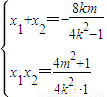 ,
,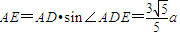 ,由以EF为直径的圆过双曲线C的右顶点D(2,0),知Rt△PAE即
,由以EF为直径的圆过双曲线C的右顶点D(2,0),知Rt△PAE即 ,由此入手能够导出直线过定点(
,由此入手能够导出直线过定点(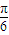 ,0).
,0).解答:解:(1)由题意设双曲线的标准方程为
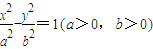 ,
,由已知得:
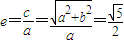 解得a=2b,
解得a=2b,∵
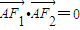 且△F1AF2的面积为1,
且△F1AF2的面积为1,∴
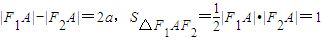 ,,|F1A|2+|F2A|2=|F1F2|2
,,|F1A|2+|F2A|2=|F1F2|2∴(|F1A|-|F2A|)2=4c2-4=4a2
∴b=1,a=2,
∴双曲线C的保准方程为
 .
.(2)设E(x1,y1),F(x2,y2) 联立y=kx+m与双曲线
| x2 |
| 4 |
得(4k2-1)x2+8kmx+4(m2+1)=0
△=(8km)2-4(4m2+4)(4k2-1)>0
即4k2-m2-1<0
则
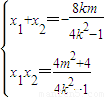 ,
,又∴
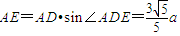
∵以EF为直径的圆过双曲线C的右顶点D(2,0)
∴Rt△PAE即

∴
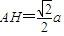
∴
 ,且均满足
,且均满足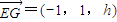 .
.∵AC1⊥EG,∴
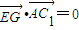 .
.当
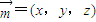 时,直线
时,直线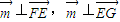 的方程为
的方程为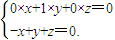 ,
,直线过定点(2,0),与已知矛盾!
当
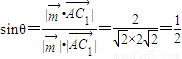 时,
时,直线
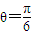 的方程为θ,直线过定点(
的方程为θ,直线过定点(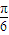 ,0)
,0)∴直线l定点,定点坐标为(
 ,0).
,0).点评:本题考查双曲线的方程的求法和求证直线l过定点,并求出该定点的坐标.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 的双曲线C的中心在坐标原点,焦点F1、F2在x轴上,双曲线C的右支上一点A使且△F1AF2的面积为1,
的双曲线C的中心在坐标原点,焦点F1、F2在x轴上,双曲线C的右支上一点A使且△F1AF2的面积为1, 的双曲线C的中心在坐标原点,左、右焦点F1、F2在x轴上,双曲线C的右支上一点A使
的双曲线C的中心在坐标原点,左、右焦点F1、F2在x轴上,双曲线C的右支上一点A使 且△F1AF2的面积为1.
且△F1AF2的面积为1.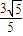 的双曲线
的双曲线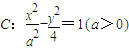 的左焦点与抛物线y2=2mx的焦点重合,则实数m= .
的左焦点与抛物线y2=2mx的焦点重合,则实数m= . 的双曲线
的双曲线 的左焦点与抛物线y2=2mx的焦点重合,则实数m= .
的左焦点与抛物线y2=2mx的焦点重合,则实数m= .