题目内容
已知离心率为
的双曲线
的左焦点与抛物线y2=2mx的焦点重合，则实数m= ．
【答案】分析：先由双曲线的离心率求出a的值，由此得到双曲线的左焦点，再求出抛物线y2=2mx的焦点坐标，利用它们复合，从而求出实数m．
解答：解：∵双曲线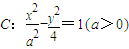
的离心率为
，
∴
=
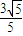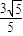⇒a2=5，
双曲线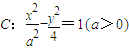
的左焦点是（-3，0），
抛物线y2=2mx的焦点（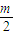
，0）
∴
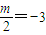⇒m=-6．
故答案为：-6．
点评：本题考查抛物线的简单性质、双曲线的性质和应用，考查了学生对基础知识的综合把握能力．属于基础题．
解答：解：∵双曲线
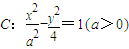的离心率为，∴
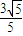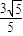=⇒a2=5，双曲线
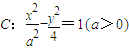的左焦点是（-3，0），抛物线y2=2mx的焦点（
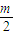，0）∴
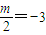⇒m=-6．故答案为：-6．
点评：本题考查抛物线的简单性质、双曲线的性质和应用，考查了学生对基础知识的综合把握能力．属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
的双曲线C的中心在坐标原点，焦点F1、F2在x轴上，双曲线C的右支上一点A使且△F1AF2的面积为1，
的双曲线C的中心在坐标原点，左、右焦点F1、F2在
轴上，双曲线C的右支上一点A使
且
的面积为1。(12分)
与双曲线C相交于E、F两点（E、F不是左右顶点），且以EF为直径的圆过双曲线C的右顶点D。求证：直线
过定点，并求出该定点的坐标。
的双曲线C的中心在坐标原点，左、右焦点F1、F2在x轴上，双曲线C的右支上一点A使
且△F1AF2的面积为1．
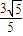的双曲线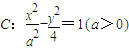
的左焦点与抛物线y2=2mx的焦点重合，则实数m= ．