题目内容
已知离心率为 的双曲线C的中心在坐标原点,焦点F1、F2在x轴上,双曲线C的右支上一点A使且△F1AF2的面积为1,
的双曲线C的中心在坐标原点,焦点F1、F2在x轴上,双曲线C的右支上一点A使且△F1AF2的面积为1,
(1)求双曲线C的标准方程;
(2)若直线l:y=kx+m与双曲线C相交于E、F两点(E、F不是左右顶点),且以EF为直径的圆过双曲线C的右顶点D,求证:直线l过定点,并求出该定点的坐标。
 的双曲线C的中心在坐标原点,焦点F1、F2在x轴上,双曲线C的右支上一点A使且△F1AF2的面积为1,
的双曲线C的中心在坐标原点,焦点F1、F2在x轴上,双曲线C的右支上一点A使且△F1AF2的面积为1,(1)求双曲线C的标准方程;
(2)若直线l:y=kx+m与双曲线C相交于E、F两点(E、F不是左右顶点),且以EF为直径的圆过双曲线C的右顶点D,求证:直线l过定点,并求出该定点的坐标。
解:(1)由题意,设双曲线的标准方程为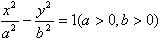 ,
,
由已知得: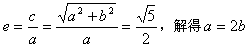 ,
,
∵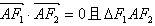 的面积为1,
的面积为1,
∴ ,
,
∴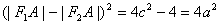 ,
,
∴b=1,a=2,
∴双曲线C的标准方程为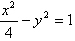 。
。
(2)设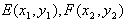 ,
,
联立 ,
,
显然 ,
,
否则直线l与双曲线C只有一个交点,
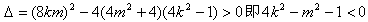 ,
,
则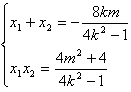 ,
,
又 ,
,
∵以EF为直径的圆过双曲线C的右顶点D(2,0),
∴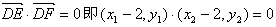 ,
,
∴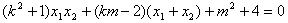 ,
,
∴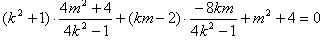 ,
,
化简整理得 ,
,
∴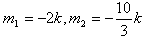 ,且均满足
,且均满足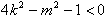 ,
,
当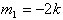 时,直线l的方程为y=k(x-2),直线过定点(2,0),与已知矛盾;
时,直线l的方程为y=k(x-2),直线过定点(2,0),与已知矛盾;
当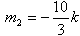 时,直线l的方程为
时,直线l的方程为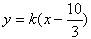 ,直线过定点(
,直线过定点(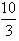 ,0);
,0);
∴直线l定点,定点坐标为(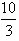 ,0)。
,0)。
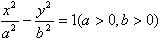 ,
,由已知得:
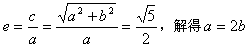 ,
,∵
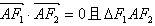 的面积为1,
的面积为1, ∴
 ,
,∴
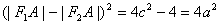 ,
,∴b=1,a=2,
∴双曲线C的标准方程为
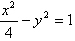 。
。(2)设
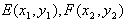 ,
,联立
 ,
,显然
 ,
,否则直线l与双曲线C只有一个交点,
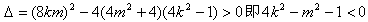 ,
,则
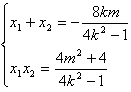 ,
,又
 ,
,∵以EF为直径的圆过双曲线C的右顶点D(2,0),
∴
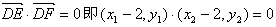 ,
,∴
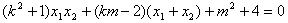 ,
,∴
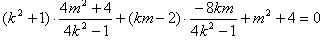 ,
,化简整理得
 ,
,∴
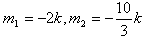 ,且均满足
,且均满足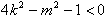 ,
,当
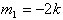 时,直线l的方程为y=k(x-2),直线过定点(2,0),与已知矛盾;
时,直线l的方程为y=k(x-2),直线过定点(2,0),与已知矛盾;当
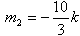 时,直线l的方程为
时,直线l的方程为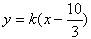 ,直线过定点(
,直线过定点(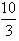 ,0);
,0); ∴直线l定点,定点坐标为(
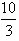 ,0)。
,0)。
练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 的双曲线C的中心在坐标原点,左、右焦点F1、F2在x轴上,双曲线C的右支上一点A使
的双曲线C的中心在坐标原点,左、右焦点F1、F2在x轴上,双曲线C的右支上一点A使 且△F1AF2的面积为1.
且△F1AF2的面积为1.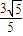 的双曲线
的双曲线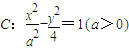 的左焦点与抛物线y2=2mx的焦点重合,则实数m= .
的左焦点与抛物线y2=2mx的焦点重合,则实数m= . 的双曲线
的双曲线 的左焦点与抛物线y2=2mx的焦点重合,则实数m= .
的左焦点与抛物线y2=2mx的焦点重合,则实数m= .