题目内容
如图,设 两点在河的两岸,一测量者在
两点在河的两岸,一测量者在 所在的同侧河岸边选定一点
所在的同侧河岸边选定一点 ,测出
,测出 的距离为
的距离为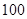
 ,
, ,
, 后,就可以计算出
后,就可以计算出 两点的距离为
两点的距离为
A. m m | B. m m | C. m m | D. m m |
D
解析试题分析:由 ,
, 得到
得到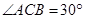 ,由正弦
,由正弦
定理得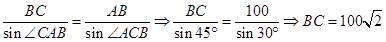
考点:正弦定理

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
锐角 中,角
中,角 所对的边长分别为
所对的边长分别为 .若
.若
A. | B. | C. | D. |
在△ABC中, 分别为角
分别为角 所对的边,若
所对的边,若 ,则△ABC的形状为( )
,则△ABC的形状为( )
| A.钝角三角形 | B.直角三角形 | C.锐角三角形 | D.不能确定 |
在△ABC中,已知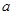 =3,c=3
=3,c=3 ,A=30°,则角C等于
,A=30°,则角C等于
| A.30° | B.60°或120° | C.60° | D.120° |
 的内角
的内角 所对的边
所对的边 满足
满足 ,且C=60°,则
,且C=60°,则 的值为( )
的值为( )
A. | B. | C.1 | D. |
已知 外接圆
外接圆 的半径为
的半径为 ,且
,且 .
. ,从圆
,从圆 内随机取一个点
内随机取一个点 ,若点
,若点 取自
取自 内的概率恰为
内的概率恰为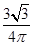 ,则
,则 的形状为( )
的形状为( )
| A.直角三角形 | B.等边三角形 | C.钝角三角形 | D.等腰直角三角形 |
若满足条件C=60°,AB= ,BC=a的△ABC有两个,那么a的取值范围是 ( )
,BC=a的△ABC有两个,那么a的取值范围是 ( )
A.(1, ) ) | B.( , , ) ) | C.( ,2) ,2) | D.(1,2) |
 中,
中, ,
,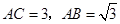 ,则
,则 ( )
( )
A. | B. | C. | D. |
设△ABC的内角A,B,C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为( )
| A.直角三角形 | B.锐角三角形 |
| C.钝角三角形 | D.不确定 |