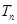题目内容
(本小题满分15分)
数列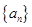 是首项为23,公差为整数的等差数列,且
是首项为23,公差为整数的等差数列,且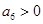 ,
,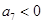 .
.
求:(1)数列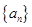 的公差;
的公差;
(2)前 项和
项和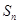 的最大值;
的最大值;
(3)当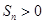 时,求
时,求 的最大值.
的最大值.
(1)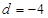 ; (2)78 ; (3)12 。
; (2)78 ; (3)12 。
解析试题分析:(1)由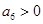 ,
,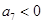 得:
得: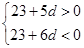 ,所以
,所以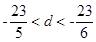 ,
,
因为公差为整数,所以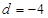 …………5分
…………5分
(2)由(1)易知,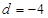 <0,
<0, 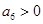 ,
,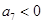 ,
,
所以前6项和最大,最大为S6=78。 …………10分
(3)由Sn=23n+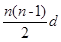 =
=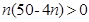 得:
得: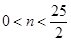 ,又n∈N*,
,又n∈N*,
所以n的最大值为12. …………15分
考点:本题考查等差数列的通项公式;等差数列的前n项和.
点评:本题以等差数列为载体,考查等差数列的性质、通项公式以及前n项和公式.正确运用等差数列通项及前n项和公式,是解题的关键.

练习册系列答案
相关题目
已知数列 中的
中的 ,且
,且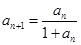 (
( ),则数列
),则数列 中的
中的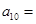 ( )
( )
A. | B. | C.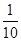 | D.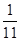 |
观察下列式子: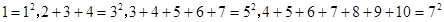 ,…,则第n个式子是( )
,…,则第n个式子是( )
A. |
B.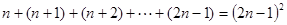 |
C.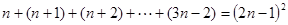 |
D.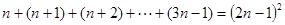 |
 满足
满足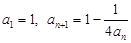 ,其中
,其中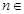 N*.
N*.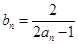 ,求证:数列
,求证:数列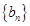 是等差数列,并求出
是等差数列,并求出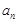 ;
; ,数列
,数列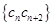 的前
的前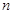 项和为
项和为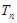 ,是否存在正整数
,是否存在正整数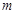 ,使得
,使得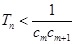 对于
对于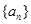 满足:
满足: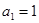 ,
,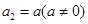 ,
,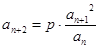 (其中
(其中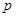 为非零常数,
为非零常数,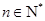 ).
). 是不是等比数列?
是不是等比数列?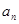 ;
;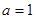 时,令
时,令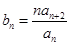 ,
,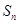 为数列
为数列 的前
的前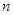 项和,求
项和,求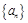 中的各项均为正数,且满足
中的各项均为正数,且满足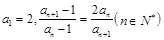 .记
.记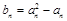 ,数列
,数列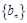 的前
的前 项和为
项和为 ,且
,且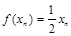 .
.  是等比数列;
是等比数列;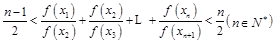 .
.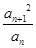 (其中P为非零常数,n∈N *)
(其中P为非零常数,n∈N *)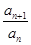 }是不是等比数列?
}是不是等比数列?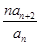 ,Sn为数列{bn}的前n项和,求Sn。
,Sn为数列{bn}的前n项和,求Sn。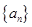 是等差数列,
是等差数列,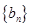 是各项为正数的等比数列,且
是各项为正数的等比数列,且 ,
,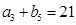 ,
,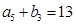 .
.  ,求数列
,求数列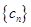 的前
的前 项和
项和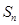 .
.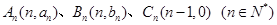 ,满足向量
,满足向量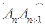 与向量
与向量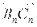 共线,且点
共线,且点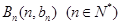 都在斜率为6的同一条直线上。若
都在斜率为6的同一条直线上。若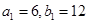 。求(1)数列
。求(1)数列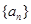 的通项
的通项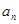 (2)数列{
(2)数列{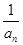 }的前n项和
}的前n项和