题目内容
若函数 的零点与
的零点与 的零点之差的绝对值不超过
的零点之差的绝对值不超过 , 则
, 则 可以是( )
可以是( )
A. | B.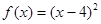 |
C. | D.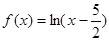 |
D
解析试题分析: 的定义域为
的定义域为 ,因为,
,因为, ,所以,其零点在区间(3,4)之间。
,所以,其零点在区间(3,4)之间。
考查选项中的函数, 与
与 的零点为2,
的零点为2,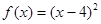 为4,
为4,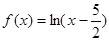 的零点为
的零点为 ,故与
,故与 的零点之差的绝对值不超过
的零点之差的绝对值不超过 的函数
的函数 应为
应为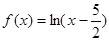 ,选D.
,选D.
考点:函数零点存在定理

练习册系列答案
相关题目
已知定义在R上的函数 满足
满足 ,
, ,且在区间
,且在区间 上是减函数.若方程
上是减函数.若方程 在区间
在区间 上有两个不同的根,则这两根之和为( )
上有两个不同的根,则这两根之和为( )
| A.±8 | B.±4 | C.±6 | D.±2 |
若存在负实数使得方程  成立,则实数
成立,则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
函数 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
设函数 有两个极值点
有两个极值点 ,且
,且 ,则 ( )
,则 ( )
A. | B. |
C. | D. |
下列函数中,值域是 的函数是( )
的函数是( )
A. | B. | C.  | D. |
若函数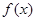 对于任意的
对于任意的 都有
都有 ,且
,且 ,则
,则 ( )
( )
A. | B. | C. | D. |
记实数 中的最大数为max{
中的最大数为max{ } , 最小数为min{
} , 最小数为min{ }则max{min{
}则max{min{ }}= ( )
}}= ( )
A. | B.1 | C.3 | D.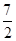 |
 的⊙
的⊙ 切直线
切直线 于
于 ,射线
,射线 从
从 出发绕着
出发绕着 .旋转过程中,
.旋转过程中, .记
.记 为
为 、弓形
、弓形 的面积为
的面积为 ,那么
,那么 的图象是下面右图中的( )
的图象是下面右图中的( )