题目内容

将函数y=sin(2x+
π
6
)的图象向左平移
π
3
个单位后得到的图象对应的解析式为y=-sin（2x+θ），则符合条件的绝对值最小的θ角是
-
π
6
-
π
6
．
分析：根据函数图象平移的公式得到平移后的图象对应的函数为y=sin(2x+
5π
6
)，说明sin(2x+
5π
6
)=-sin（2x+θ）对任意的x∈R恒成立，再根据正弦的诱导公式得到θ满足的等式，从而找出符合条件的绝对值最小的θ角．
解答：解：设y=f(x)=sin(2x+
π
6
)，可得将函数y=sin(2x+
π
6
)的图象向左平移
π
3
个单位，
得到f(x+
π
3
)=sin[2(x+
π
3
)+
π
6
]=sin(2x+
5π
6
)的图象，
∴结合题意，可得sin(2x+
5π
6
)=-sin（2x+θ）对任意的x∈R恒成立，
根据诱导公式可得：π+2x+θ=2x+
5π
6
+2kπ（k∈Z），即θ=-
π
6
+2kπ（k∈Z），
当k=0时，绝对值最小的θ=-
π
6
．
故答案为：-
π
6
点评：本题给出正弦型函数图象的平移，求符合条件的角θ的值．着重考查了诱导公式、三角函数的图象与性质、函数图象的平移公式等知识，属于基础题．
练习册系列答案
相关题目
给出下列命题：
①在△ABC中，若A＜B，则sinA＜sinB；
②将函数y=sin(2图象向右平移
π
3
个单位，得到函数y=sin2x的图象；
③在△ABC中，若AB=2，AC=3，∠ABC=60°，则△ABC必为锐角三角形；
④在同一坐标系中，函数y=sinx的图象和函数y=
x
2
的图象有三个公共点．
其中真命题是
 
．（填出所有正确命题的序号）
将函数y=sin(6x+
π
4
)的图象上各点的横坐标伸长到原来的3倍，再向右平移
π
8
个单位，得到的函数的一个对称中心（　　）
将函数y=sin(x+
π
3
)的图象向右平移
π
6
个单位，再向上平移2个单位所得图象对应的函数解析式是
y=sin(x+
π
6
)+2
y=sin(x+
π
6
)+2
．
将函数y=sin(
1
2
x+
π
3
)的图象作如下那种变换，才能得到函数y=sin(
1
2
x)的图象（　　）

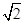要得到函数y=cos(2+)的图象, 只需要将函数y=sin(2+)图象上所有的点(     )

A．向左平移个单位，纵坐标不变；

B．向右平移个单位，纵坐标不变；

C．向左平移个单位，纵坐标不变；

D．向右平移 个单位，纵坐标不变．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网