题目内容
14.己知实数x、y满足$\left\{\begin{array}{l}{y≤x}\\{x+2y≤4}\\{y≥-2}\end{array}\right.$,若存在x、y满足(x+1)2+(y-1)2=r2(r>0),则r的最小值为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{4}{3}$$\sqrt{2}$ | D. | $\frac{4}{3}$$\sqrt{3}$ |
分析 画出满足约束条件的可行域,分析(x+1)2+(y-1)2=r2(r>0)中r的几何意义,数形结合,可得答案.
解答 解:满足约束条件$\left\{\begin{array}{l}{y≤x}\\{x+2y≤4}\\{y≥-2}\end{array}\right.$的可行域如下图所示: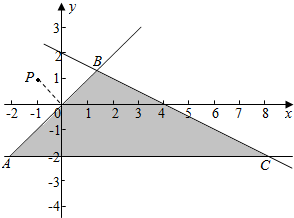
(x+1)2+(y-1)2表示P(-1,1)到平面区间内一点(x,y)距离的平方,
由P到直线y=x的距离为$\sqrt{2}$,
可得r的最小值为$\sqrt{2}$,
故选:A.
点评 本题考查的知识点是线性规划的简单应用,画出满足条件的可行域,是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7. 已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<π)的一段图象如图所示,则过点P(ω,φ),且斜率为A的直线方程是( )
已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<π)的一段图象如图所示,则过点P(ω,φ),且斜率为A的直线方程是( )
 已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<π)的一段图象如图所示,则过点P(ω,φ),且斜率为A的直线方程是( )
已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<π)的一段图象如图所示,则过点P(ω,φ),且斜率为A的直线方程是( )| A. | y-$\frac{π}{3}$=$\sqrt{3}$(x-2) | B. | y-$\frac{2π}{3}$=$\sqrt{3}$(x-4) | C. | y-$\frac{2π}{3}$=2(x-4) | D. | y-$\frac{2π}{3}$=2(x-2) |
 如图所示,在四棱锥P-ABCD中,△PAB为等边三角形,AD⊥AB,AD∥BC,平面PAB⊥平面ABCD,E为PD的中点,F为PA中点.
如图所示,在四棱锥P-ABCD中,△PAB为等边三角形,AD⊥AB,AD∥BC,平面PAB⊥平面ABCD,E为PD的中点,F为PA中点.