题目内容
9. 如图,已知点C是以AB为直径的半圆O上一点,过C的直线交AB的延长线于E,交过点A的圆O的切线于点D,BC∥OD,AD=AB=2.
如图,已知点C是以AB为直径的半圆O上一点,过C的直线交AB的延长线于E,交过点A的圆O的切线于点D,BC∥OD,AD=AB=2.(Ⅰ)求证:直线DC是圆O的切线;
(Ⅱ)求线段EB的长.
分析 (Ⅰ)要证DE是圆O的切线,连接AC,只需证出∠DAO=90°,由BC∥OD⇒OD⊥AC,则OD是AC的中垂线.通过△AOC,△BOC均为等腰三角形,即可证得∠DAO=90°.
(Ⅱ)由 BC∥OD⇒∠CBA=∠DOA,结合∠BCA=∠DAO,得出△ABC∽△AOD,利用比例线段求出EB.
解答 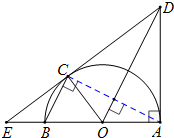 (Ⅰ)证明:连接AC,AB是直径,则BC⊥AC,
(Ⅰ)证明:连接AC,AB是直径,则BC⊥AC,
由BC∥OD⇒OD⊥AC,
则OD是AC的中垂线⇒∠OCA=∠OAC,∠DCA=∠DAC,
⇒∠OCD=∠OCA+∠DCA=∠OAC+∠DAC=∠DAO=90°.
⇒OC⊥DE,所以DE是圆O的切线.
(Ⅱ)解:BC∥OD⇒∠CBA=∠DOA,∠BCA=∠DAO⇒△ABC∽△AOD
⇒$\frac{BC}{OA}=\frac{AB}{OD}$⇒BC=$\frac{OA•AB}{OD}$=$\frac{2\sqrt{5}}{5}$⇒$\frac{BC}{OD}$=$\frac{2}{5}$⇒$\frac{BE}{OE}$=$\frac{2}{5}$⇒$\frac{BE}{OB}$=$\frac{2}{3}$⇒BE=$\frac{2}{3}$.
点评 本题考查圆的切线的证明,与圆有关的比例线段.准确掌握与圆有关的线、角的性质是解决此类问题的基础和关键.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
19.已知△ABC中,内角A,B,C所对的边长分别为a,b,c,若$A=\frac{π}{3}$,且b=2acosB,c=1,则△ABC的面积等于( )
| A. | $\frac{{\sqrt{3}}}{4}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{6}$ | D. | $\frac{{\sqrt{3}}}{8}$ |
20.类比平面内“垂直于同一条直线的两条直线互相平行”的性质,可得出空间内的下列结论:( )
①垂直于同一个平面的两条直线互相平行;
②垂直于同一条直线的两条直线互相平行;
③垂直于同一个平面的两个平面互相平行;
④垂直于同一条直线的两个平面互相平行.
①垂直于同一个平面的两条直线互相平行;
②垂直于同一条直线的两条直线互相平行;
③垂直于同一个平面的两个平面互相平行;
④垂直于同一条直线的两个平面互相平行.
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
4.已知某空间几何体的三视图如图所示,则该几何体的体积是( )
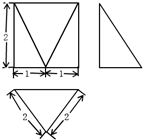

| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{5\sqrt{3}}{3}$ |
1.设x1,x2,x3均为实数,且 $(\frac{1}{3})^{{x}_{1}}$=log2(x1+1),$(\frac{1}{3})^{{x}_{2}}$=log3x2,$(\frac{1}{3})^{{x}_{3}}$=log2x3,则( )
| A. | x1<x3<x2 | B. | x3<x2<x1 | C. | x3<x1<x2 | D. | x3<x1<x2 |