题目内容
1．设x1，x2，x3均为实数，且 $（\frac{1}{3}）^{{x}_{1}}$=log2（x1+1），$（\frac{1}{3}）^{{x}_{2}}$=log3x2，$（\frac{1}{3}）^{{x}_{3}}$=log2x3，则（ ）| A． | x1＜x3＜x2 | B． | x3＜x2＜x1 | C． | x3＜x1＜x2 | D． | x3＜x1＜x2 |
分析 利用指数函数与对数函数的图象与性质画出图象，即可得出结论．
解答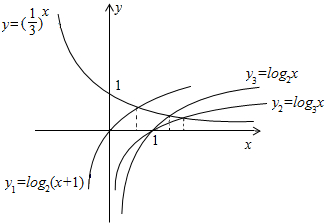 
解：如图所示，
由图象可知：x1＜x3＜x2．
故选：A．
点评 本题考查了指数函数与对数函数的图象与性质，属于基础题．
练习册系列答案
互动英语系列答案
相关题目
11．已知等差数列{an}的公差d≠0，且a3=2a1，则$\frac{{{a_1}+{a_3}}}{{{a_2}+{a_4}}}$的值为（ ）
| A． | $\frac{5}{6}$ | B． | $\frac{4}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{2}{3}$ |
12．某出租车公司响应国家节能减排的号召，已陆续购买了140辆纯电动汽车作为运营车辆，目前我国主流纯电动汽车按续驶里程数R（单位：公里）分为3类，即A：80≤R＜150，B：150≤R＜250，C：R≥250．对这140辆车的行驶总里程进行统计，结果如下表：
（Ⅰ）从这140辆汽车中任取1辆，求该车行驶总里程超过5万公里的概率；
（Ⅱ）公司为了了解这些车的工作状况，决定抽取14辆车进行车况分析，按表中描述的六种情况进行分层抽样，设从C类车中抽取了n辆车．
（ⅰ）求n的值；
（ⅱ）如果从这n辆车中随机选取2辆车，求恰有1辆车行驶总里程超过5万公里的概率．
| 类型 | A | B | C |
| 已行驶总里程不超过5万公里的车辆数 | 10 | 40 | 30 |
| 已行驶总里程超过5万公里的车辆数 | 20 | 20 | 20 |
（Ⅱ）公司为了了解这些车的工作状况，决定抽取14辆车进行车况分析，按表中描述的六种情况进行分层抽样，设从C类车中抽取了n辆车．
（ⅰ）求n的值；
（ⅱ）如果从这n辆车中随机选取2辆车，求恰有1辆车行驶总里程超过5万公里的概率．
如图，已知点C是以AB为直径的半圆O上一点，过C的直线交AB的延长线于E，交过点A的圆O的切线于点D，BC∥OD，AD=AB=2．
16．已知非零向量$\overrightarrow{AB}$和$\overrightarrow{BP}$，又知$\overrightarrow{BP}$=$\overrightarrow{AB}$，则点P与AB的关系是（ ）
| A． | P在直线AB外 | B． | P在AB延长线上 | C． | P点与B点重合 | D． | 以上都有可能 |
13．函数f（x）=2sin（x-$\frac{π}{6}$）cos（x-$\frac{π}{6}$）图象的一条对称轴方程是（ ）
| A． | x=$\frac{π}{6}$ | B． | x=$\frac{π}{3}$ | C． | x=$\frac{5π}{12}$ | D． | x=$\frac{2π}{3}$ |
10．“方程$\frac{{x}^{2}}{k-2}$+$\frac{{y}^{2}}{k-5}$=1表示的曲线是双曲线”是“2＜k＜5”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不充要条件 |