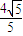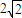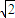题目内容
如果点P在平面区域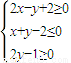 内,点Q在曲线x2+y2-4x-4y+7=0上,则|PQ|的最小值为( )
内,点Q在曲线x2+y2-4x-4y+7=0上,则|PQ|的最小值为( )A.2
B.
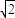
C.
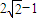
D.
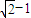
【答案】分析:先将曲线x2+y2-4x-4y+7=0化成圆的标准方程,得到Q在以点C(2,2)为圆心,半径为1的圆上运动.然后作出题中不等式组对应的平面区域,作出点C到区域边界的直线AD:x+y-2=0的垂线,可得当点P与垂足重合,且动点Q恰好落在垂线与圆C的交点时,|PQ|达到最小值.最后用点到直线的距离公式,可以算出点C到直线AD的距离,从而得到|PQ|的最小值为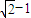 .
.
解答:解:曲线x2+y2-4x-4y+7=0化成(x-2)2+(y-2)2=1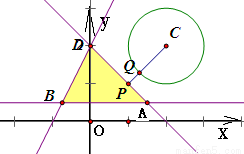
得圆的标准方程,曲线表示的是以C(2,2)为圆心,半径为1的圆.
因此|PQ|的最小值,化为先求点C到平面区域 内点的最小值,再用这个最小值减去半径1即可.
内点的最小值,再用这个最小值减去半径1即可.
作出平面区域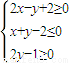 ,如右图△BAD及其内部
,如右图△BAD及其内部
过点C作出直线AD:x+y-2=0的垂线,
当点P与垂足重合,且动点Q恰好落在垂线与圆C的交点时,
|PQ|达到最小值.
∵点C(2,2)到直线AD:x+y-2=0的距离为d=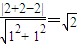
∴|PQ|的最小值为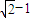
故选D
点评:本题以圆上的动点到三角形区域内点的最小距离问题为载体,着重考查了简单线性规划的应用、圆的标准方程和点到直线距离公式等知识点,属于中档题.
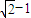 .
.解答:解:曲线x2+y2-4x-4y+7=0化成(x-2)2+(y-2)2=1

得圆的标准方程,曲线表示的是以C(2,2)为圆心,半径为1的圆.
因此|PQ|的最小值,化为先求点C到平面区域
 内点的最小值,再用这个最小值减去半径1即可.
内点的最小值,再用这个最小值减去半径1即可.作出平面区域
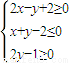 ,如右图△BAD及其内部
,如右图△BAD及其内部过点C作出直线AD:x+y-2=0的垂线,
当点P与垂足重合,且动点Q恰好落在垂线与圆C的交点时,
|PQ|达到最小值.
∵点C(2,2)到直线AD:x+y-2=0的距离为d=
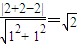
∴|PQ|的最小值为
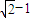
故选D
点评:本题以圆上的动点到三角形区域内点的最小距离问题为载体,着重考查了简单线性规划的应用、圆的标准方程和点到直线距离公式等知识点,属于中档题.

练习册系列答案
相关题目
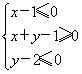 内,点Q在曲线(x+2)2+y2=1上,那么|PQ|的最大值为________.
内,点Q在曲线(x+2)2+y2=1上,那么|PQ|的最大值为________.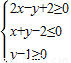 内,点Q在曲线
内,点Q在曲线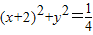 上,那么|PQ|的最小值为( )
上,那么|PQ|的最小值为( )
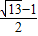
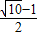
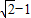
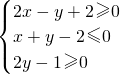 内,点Q(0,-2),那么|PQ|的最小值为
内,点Q(0,-2),那么|PQ|的最小值为



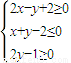 内,点Q(0,-2),那么|PQ|的最小值为( )
内,点Q(0,-2),那么|PQ|的最小值为( )