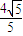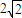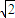题目内容
如果点P在平面区域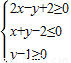 内,点Q在曲线
内,点Q在曲线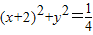 上,那么|PQ|的最小值为( )
上,那么|PQ|的最小值为( )A.

B.
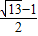
C.
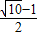
D.
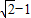
【答案】分析:作出可行域,将|PQ|的最小值转化为圆心到可行域的最小值,结合图形,求出|CP|的最小值,减去半径得|PQ|的最小值.
解答:解析:如图,画出平面区域(阴影部分所示),由圆心C(-2,0)向直线3x+4y-4=0作垂线,
圆心C(-2,0)到点(- ,1)的距离为
,1)的距离为 ,又圆的半径为
,又圆的半径为 ,所以可求得|PQ|的最小值是
,所以可求得|PQ|的最小值是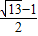 .
.
故选B
点评:本题考查简单的线性规划问题,本题解题的关键是看清楚条件中所表示的几何意义,实际上是求两点之间的距离的最值,本题是一个基础题.
解答:解析:如图,画出平面区域(阴影部分所示),由圆心C(-2,0)向直线3x+4y-4=0作垂线,

圆心C(-2,0)到点(-
 ,1)的距离为
,1)的距离为 ,又圆的半径为
,又圆的半径为 ,所以可求得|PQ|的最小值是
,所以可求得|PQ|的最小值是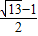 .
.故选B
点评:本题考查简单的线性规划问题,本题解题的关键是看清楚条件中所表示的几何意义,实际上是求两点之间的距离的最值,本题是一个基础题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
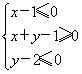 内,点Q在曲线(x+2)2+y2=1上,那么|PQ|的最大值为________.
内,点Q在曲线(x+2)2+y2=1上,那么|PQ|的最大值为________.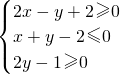 内,点Q(0,-2),那么|PQ|的最小值为
内,点Q(0,-2),那么|PQ|的最小值为



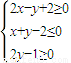 内,点Q在曲线x2+y2-4x-4y+7=0上,则|PQ|的最小值为( )
内,点Q在曲线x2+y2-4x-4y+7=0上,则|PQ|的最小值为( )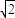
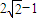
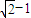
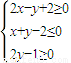 内,点Q(0,-2),那么|PQ|的最小值为( )
内,点Q(0,-2),那么|PQ|的最小值为( )