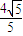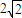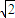题目内容
如果点P在平面区域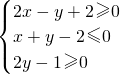
内，点Q（0，-2），那么|PQ|的最小值为
- A.
- B.
- C.
- D.
B
分析：先根据约束条件画出区域图，然后根据|PQ|的几何意义就是平面区域内一点P到Q的距离，结合图形可得最小值为|CQ|，最后利用两点的距离公式解之即可．
解答：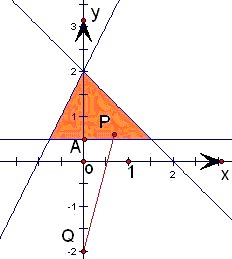
解：根据约束条件 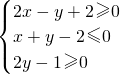画出平面区域，
|PQ|的几何意义就是平面区域内一点P到Q的距离
观察图形，
当点P在点A（0，
）处|PQ|取最小值
∴|PQ|的最小值为
故选B．
点评：本题考查的知识点是简单线性规划，其中根据约束条件画出可行域，并分析目标函数的几何意义是解答本题的关键．
分析：先根据约束条件画出区域图，然后根据|PQ|的几何意义就是平面区域内一点P到Q的距离，结合图形可得最小值为|CQ|，最后利用两点的距离公式解之即可．
解答：
解：根据约束条件 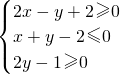画出平面区域，|PQ|的几何意义就是平面区域内一点P到Q的距离
观察图形，
当点P在点A（0，
）处|PQ|取最小值∴|PQ|的最小值为
故选B．
点评：本题考查的知识点是简单线性规划，其中根据约束条件画出可行域，并分析目标函数的几何意义是解答本题的关键．
练习册系列答案
相关题目
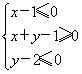内，点Q在曲线(x＋2)2＋y2＝1上，那么|PQ|的最大值为________．
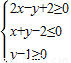内，点Q在曲线
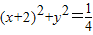上，那么|PQ|的最小值为（ ）
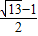
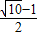
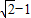
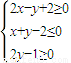内，点Q在曲线x2+y2-4x-4y+7=0上，则|PQ|的最小值为（ ）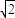
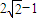
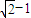
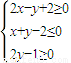内，点Q（0，-2），那么|PQ|的最小值为（ ）
