题目内容
在一次电视节目的抢答中,题型为判断题,只有“对”和“错”两种结果,其中某明星判断正确的概率为p,判断错误的概率为q,若判断正确则加1分,判断错误则减1分,现记“该明星答完n题后总得分为Sn”.(1)当p=q=
| 1 |
| 2 |
(2)当p=
| 1 |
| 3 |
| 2 |
| 3 |
分析:(1)由题意知变量的可能取值是1,3,结合变量对应的事件和独立重复试验的概率公式写出变量对应的概率和分布列,做出期望和方差.
(2)本题要求的概率是答完8题后,回答正确的题数为5题,回答错误的题数是3题,包括若第一题和第二题回答正确,则其余6题可任意答对3题;和若第一题正确和第二题回答错误,第三题回答正确,则后5题可任意答对3题,两种情况,写出概率.
(2)本题要求的概率是答完8题后,回答正确的题数为5题,回答错误的题数是3题,包括若第一题和第二题回答正确,则其余6题可任意答对3题;和若第一题正确和第二题回答错误,第三题回答正确,则后5题可任意答对3题,两种情况,写出概率.
解答:解:(1)∵ξ=|S3|的取值为1,3,又p=q=
;
∴P(ξ=1)=2
(
)•(
)2=
,
P(ξ=3)=(
)3+(
)3=
.
∴ξ的分布列为:
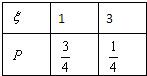
∴Eξ=1×
+3×
=
;
Dξ=
×(1-
)2+
×(3-
)2=
(2)当S 8=2时,即答完8题后,回答正确的题数为5题,回答错误的题数是3题,
又已知Si≥0(i=1,2,3,4),若第一题和第二题回答正确,则其余6题可任意答对3题;
若第一题正确,第二题回答错误,第三题回答正确,则后5题可任意答对3题.
此时的概率为P=(
+
)•(
)5•(
)3=
=
(或
).
| 1 |
| 2 |
∴P(ξ=1)=2
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
P(ξ=3)=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴ξ的分布列为:

∴Eξ=1×
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
Dξ=
| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
(2)当S 8=2时,即答完8题后,回答正确的题数为5题,回答错误的题数是3题,
又已知Si≥0(i=1,2,3,4),若第一题和第二题回答正确,则其余6题可任意答对3题;
若第一题正确,第二题回答错误,第三题回答正确,则后5题可任意答对3题.
此时的概率为P=(
| C | 3 6 |
| C | 3 5 |
| 1 |
| 3 |
| 2 |
| 3 |
| 30×8 |
| 38 |
| 80 |
| 37 |
| 80 |
| 2187 |
点评:本题考查离散型随机变量的分布列和期望,这种类型是近几年高考题中经常出现的,考查离散型随机变量的分布列和期望,大型考试中理科考试必出的一道问题.

练习册系列答案
相关题目
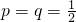 时,记ξ=|S3|,求ξ的分布列及数学期望及方差;
时,记ξ=|S3|,求ξ的分布列及数学期望及方差;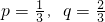 时,求S8=2且Si≥0(i=1,2,3,4)的概率.
时,求S8=2且Si≥0(i=1,2,3,4)的概率.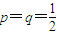 时,记ξ=|S3|,求ξ的分布列及数学期望及方差;
时,记ξ=|S3|,求ξ的分布列及数学期望及方差;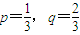 时,求S8=2且Si≥0(i=1,2,3,4)的概率.
时,求S8=2且Si≥0(i=1,2,3,4)的概率.