题目内容
设函数f(x)=
,
(1)画出此函数的图象;
(2)若f(x)=-1,求x的值;
(3)若f(x)<0,求x的取值范围;
(4)若f(x+1)≥-
,求实数x的取值范围.
|
(1)画出此函数的图象;
(2)若f(x)=-1,求x的值;
(3)若f(x)<0,求x的取值范围;
(4)若f(x+1)≥-
| 1 |
| 2 |
分析:(1)根据一次函数和反比例函数的图象和性质,分段画出函数的图象,可得到整个函数的图象;
(2)分段构造方程f(x)=-1,解答后,综合分类讨论结合可得f(x)=-1时x的值;
(3)分段构造不等式f(x)<0,解答后,综合分类讨论结合可得f(x)<0时x的取值范围;
(4)分段构造不等式f(x+1)≥-
,解答后,综合分类讨论结合可得f(x+1)≥-
,时x的取值范围.
(2)分段构造方程f(x)=-1,解答后,综合分类讨论结合可得f(x)=-1时x的值;
(3)分段构造不等式f(x)<0,解答后,综合分类讨论结合可得f(x)<0时x的取值范围;
(4)分段构造不等式f(x+1)≥-
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)函数f(x)=
的图象如下图所示,
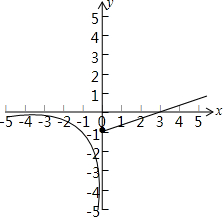
(2)当x≥0时,f(x)=
x-1=-1,解得x=0
当x<0时,f(x)=
=-1,解得x=-1
综上所述,f(x)=-1时,x值为0或-1
(3)当x≥0时,f(x)=
x-1<0,解得0≤x<3
当x<0时,f(x)=
<0恒成立
综上所述,f(x)<0时,x<3,
即x的取值范围为{x|x<3},
(4)当x+1≥0时,f(x+1)=
(x+1)-1≥-
,解得x≥
当x+1<0时,f(x+1)=
≥-
,解得x≤-3
综上所述,f(x+1)≥-
时,实数x的取值范围为{x|x≥
或x≤-3},
|
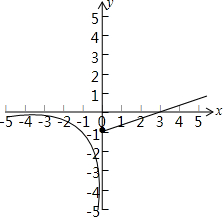
(2)当x≥0时,f(x)=
| 1 |
| 3 |
当x<0时,f(x)=
| 1 |
| x |
综上所述,f(x)=-1时,x值为0或-1
(3)当x≥0时,f(x)=
| 1 |
| 3 |
当x<0时,f(x)=
| 1 |
| x |
综上所述,f(x)<0时,x<3,
即x的取值范围为{x|x<3},
(4)当x+1≥0时,f(x+1)=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
当x+1<0时,f(x+1)=
| 1 |
| x+1 |
| 1 |
| 2 |
综上所述,f(x+1)≥-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的知识点是函数单调性的性质,函数的图象,熟练掌握分段函数的解答方法是关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目