题目内容
已知函数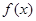 是定义在
是定义在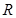 上不恒为
上不恒为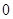 的函数,且对于任意的实数
的函数,且对于任意的实数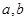 满足
满足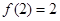 ,
,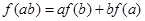 ,
,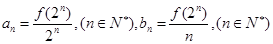 ,考察下列结论:①
,考察下列结论:①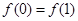 ②
②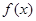 为奇函数 ③数列
为奇函数 ③数列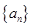 为等差数列 ④数列
为等差数列 ④数列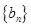 为等比数列,其中正确的个数为( )
为等比数列,其中正确的个数为( )
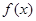 是定义在
是定义在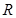 上不恒为
上不恒为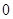 的函数,且对于任意的实数
的函数,且对于任意的实数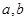 满足
满足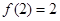 ,
,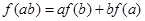 ,
,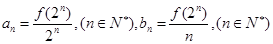 ,考察下列结论:①
,考察下列结论:①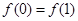 ②
②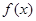 为奇函数 ③数列
为奇函数 ③数列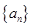 为等差数列 ④数列
为等差数列 ④数列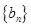 为等比数列,其中正确的个数为( )
为等比数列,其中正确的个数为( )A. | B. | C. | D. |
D
令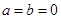 可得
可得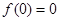 ,再令
,再令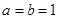 可得
可得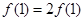 ,则
,则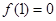 ,所以
,所以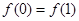 ,①正确;
,①正确;
令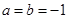 可得
可得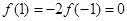 ,则
,则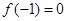 。再令
。再令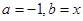 可得
可得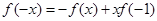 ,即
,即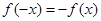 ,所以
,所以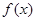 是奇函数,②正确;
是奇函数,②正确;
因为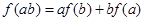 ,所以
,所以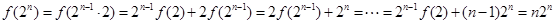
从而可得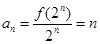 ,所以数列
,所以数列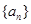 是等差数列,③正确;
是等差数列,③正确;
由上可得,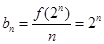 ,所以数列
,所以数列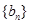 是等比数列,④正确。
是等比数列,④正确。
综上可得,故选D
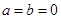 可得
可得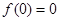 ,再令
,再令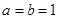 可得
可得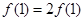 ,则
,则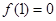 ,所以
,所以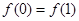 ,①正确;
,①正确;令
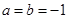 可得
可得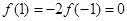 ,则
,则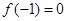 。再令
。再令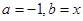 可得
可得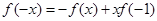 ,即
,即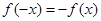 ,所以
,所以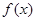 是奇函数,②正确;
是奇函数,②正确;因为
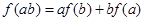 ,所以
,所以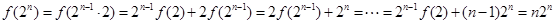
从而可得
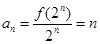 ,所以数列
,所以数列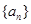 是等差数列,③正确;
是等差数列,③正确;由上可得,
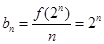 ,所以数列
,所以数列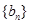 是等比数列,④正确。
是等比数列,④正确。综上可得,故选D

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
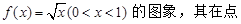
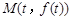
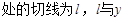 轴和直线
轴和直线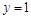 分别交于点P、Q,点N(0,1),若△PQN的面积为b时的点M恰好有两个,则b的取值范围为 ( ▲ )
分别交于点P、Q,点N(0,1),若△PQN的面积为b时的点M恰好有两个,则b的取值范围为 ( ▲ )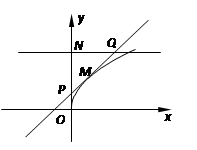
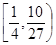
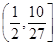
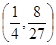
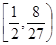
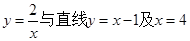 所围成的封闭图形的面积为
所围成的封闭图形的面积为 
 是函数
是函数 的极值点,其中
的极值点,其中 是自然对数的底数。
是自然对数的底数。 同时满足:
同时满足: 处的切线 ,
处的切线 ,  的图象
的图象 相切于点
相切于点
 ,求实数b的取值范围
,求实数b的取值范围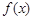 是定义在
是定义在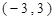 上的奇函数,当
上的奇函数,当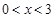 时,
时,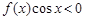 的解集是
的解集是 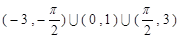
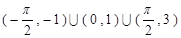
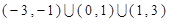
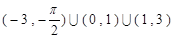
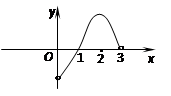
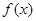 的定义域是
的定义域是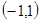 ,对于任意的
,对于任意的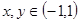 ,有
,有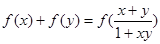 ,且当
,且当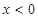 时,
时,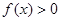 .
.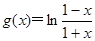 是否满足上述这些条件;
是否满足上述这些条件;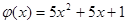
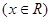 ,函数
,函数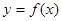 的图象与
的图象与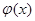 的图象关于点
的图象关于点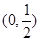 中心对称。
中心对称。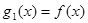 ,
,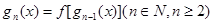 ,试求出使
,试求出使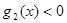 成立的
成立的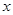 取值范围;
取值范围;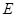 ,使
,使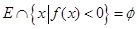 对于区间内的任意实数
对于区间内的任意实数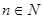 且
且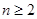 时,都有
时,都有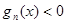 恒成立?
恒成立?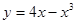 在点(-1,-3)处的切线方程是 ( ▲ )
在点(-1,-3)处的切线方程是 ( ▲ )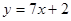
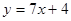
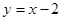
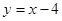
 在
在 处的切线方程为 .
处的切线方程为 .