题目内容
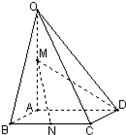
 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=| π | 4 |
(Ⅰ)证明:直线MN∥平面OCD;
(Ⅱ)求异面直线AB与MD所成角的大小;
(Ⅲ)求点B到平面OCD的距离.
分析:方法一:(1)取OB中点E,连接ME,NE,证明平面MNE∥平面OCD,方法是两个平面内相交直线互相平行得到,从而的到MN∥平面OCD;
(2)∵CD∥AB,∴∠MDC为异面直线AB与MD所成的角(或其补角)作AP⊥CD于P,连接MP
∵OA⊥平面ABCD,∴CD⊥MP菱形的对角相等得到∠ABC=∠ADC=
,
利用菱形边长等于1得到DP=
,而MD利用勾股定理求得等于
,在直角三角形中,利用三角函数定义求出即可.
(3)AB∥平面OCD,∴点A和点B到平面OCD的距离相等,连接OP,过点A作AQ⊥OP于点Q,
∵AP⊥CD,OA⊥CD,∴CD⊥平面OAP,∴AQ⊥CD,
又∵AQ⊥OP,∴AQ⊥平面OCD,线段AQ的长就是点A到平面OCD的距离,求出距离可得.
方法二:(1)分别以AB,AP,AO所在直线为x,y,z轴建立坐标系,分别表示出A,B,O,M,N的坐标,
求出
,
,
的坐标表示.设平面OCD的法向量为
=(x,y,z),则n•
=0,n•
=0,
解得
•n=(1-
,
,-1)•(0,4,
)=0,∴MN∥平面OCD
(2)设AB与MD所成的角为θ,表示出
和
,利用a•b=|a||b|cosα求出叫即可.
(3)设点B到平面OCD的距离为d,则d为
在向量n=(0,4,
)上的投影的绝对值,由
=(1,0,-2),
得d=
=
.所以点B到平面OCD的距离为
.
(2)∵CD∥AB,∴∠MDC为异面直线AB与MD所成的角(或其补角)作AP⊥CD于P,连接MP
∵OA⊥平面ABCD,∴CD⊥MP菱形的对角相等得到∠ABC=∠ADC=
| π |
| 4 |
利用菱形边长等于1得到DP=
| ||
| 2 |
| 2 |
(3)AB∥平面OCD,∴点A和点B到平面OCD的距离相等,连接OP,过点A作AQ⊥OP于点Q,
∵AP⊥CD,OA⊥CD,∴CD⊥平面OAP,∴AQ⊥CD,
又∵AQ⊥OP,∴AQ⊥平面OCD,线段AQ的长就是点A到平面OCD的距离,求出距离可得.
方法二:(1)分别以AB,AP,AO所在直线为x,y,z轴建立坐标系,分别表示出A,B,O,M,N的坐标,
求出
| MN |
| OP |
| OD |
| n |
| OP |
| OD |
解得
| MN |
| ||
| 4 |
| ||
| 4 |
| 2 |
(2)设AB与MD所成的角为θ,表示出
| AB |
| MD |
(3)设点B到平面OCD的距离为d,则d为
| OB |
| 2 |
| OB |
得d=
|
| ||
| |n| |
| 2 |
| 3 |
| 2 |
| 3 |
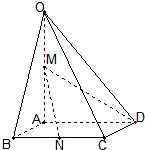
解答: 解:方法一(综合法)
解:方法一(综合法)
(1)取OB中点E,连接ME,NE
∵ME∥AB,AB∥CD,∴ME∥CD
又∵NE∥OC,∴平面MNE∥平面OCD∴MN∥平面OCD
(2)∵CD∥AB,∴∠MDC为异面直线AB与MD所成的角(或其补角)
作AP⊥CD于P,连接MP
∵OA⊥平面ABCD,∴CD⊥MP
∵∠ADP=
,∴DP=
,MD=
=
,
∴cos∠MDP=
=
,∠MDC=∠MDP=
所以AB与MD所成角的大小为
.
(3)∵AB∥平面OCD,
∴点A和点B到平面OCD的距离相等,连接OP,过点A作AQ⊥OP于点Q,
∵AP⊥CD,OA⊥CD,
∴CD⊥平面OAP,∴AQ⊥CD.
又∵AQ⊥OP,∴AQ⊥平面OCD,线段AQ的长就是点A到平面OCD的距离,
∵OP=
=
=
=
,AP=DP=
,
∴AQ=
=
=
,所以点B到平面OCD的距离为
.
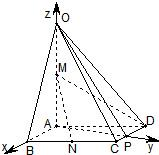 方法二(向量法)
方法二(向量法)
作AP⊥CD于点P,如图,分别以AB,AP,AO所在直线为x,y,z轴建立坐标系:
A(0,0,0),B(1,0,0),P(0,
,0),D(-
,
,0),
O(0,0,2),M(0,0,1),N(1-
,
,0)
(1)
=(1-
,
,-1),
=(0,
,-2),
=(-
,
,-2)
设平面OCD的法向量为n=(x,y,z),则
•
=0,
•
=0
即
取z=
,解得
∵
•
=(1-
,
,-1)•(0,4,
)=0,
∴MN∥平面OCD.
(2)设AB与MD所成的角为θ,
∵
=(1,0,0),
=(-
,
,-1)
∴cosθ=
=
,
∴θ=
,AB与MD所成角的大小为
.
(3)设点B到平面OCD的距离为d,则d为
在向量
=(0,4,
)上的投影的绝对值,
由
=(1,0,-2),得d=
=
所以点B到平面OCD的距离为
.
 解:方法一(综合法)
解:方法一(综合法)(1)取OB中点E,连接ME,NE
∵ME∥AB,AB∥CD,∴ME∥CD
又∵NE∥OC,∴平面MNE∥平面OCD∴MN∥平面OCD
(2)∵CD∥AB,∴∠MDC为异面直线AB与MD所成的角(或其补角)
作AP⊥CD于P,连接MP
∵OA⊥平面ABCD,∴CD⊥MP
∵∠ADP=
| π |
| 4 |
| ||
| 2 |
| MA2+AD2 |
| 2 |
∴cos∠MDP=
| DP |
| MD |
| 1 |
| 2 |
| π |
| 3 |
所以AB与MD所成角的大小为
| π |
| 3 |
(3)∵AB∥平面OCD,
∴点A和点B到平面OCD的距离相等,连接OP,过点A作AQ⊥OP于点Q,
∵AP⊥CD,OA⊥CD,
∴CD⊥平面OAP,∴AQ⊥CD.
又∵AQ⊥OP,∴AQ⊥平面OCD,线段AQ的长就是点A到平面OCD的距离,
∵OP=
| OD2-DP2 |
| OA2+AD2-DP2 |
4+1-
|
3
| ||
| 2 |
| ||
| 2 |
∴AQ=
| OA•AP |
| OP |
2•
| ||||
|
| 2 |
| 3 |
| 2 |
| 3 |
 方法二(向量法)
方法二(向量法)作AP⊥CD于点P,如图,分别以AB,AP,AO所在直线为x,y,z轴建立坐标系:
A(0,0,0),B(1,0,0),P(0,
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
O(0,0,2),M(0,0,1),N(1-
| ||
| 4 |
| ||
| 4 |
(1)
| MN |
| ||
| 4 |
| ||
| 4 |
| OP |
| ||
| 2 |
| OD |
| ||
| 2 |
| ||
| 2 |
设平面OCD的法向量为n=(x,y,z),则
| n |
| OP |
| n |
| OD |
即
|
取z=
| 2 |
∵
| MN |
| n |
| ||
| 4 |
| ||
| 4 |
| 2 |
∴MN∥平面OCD.
(2)设AB与MD所成的角为θ,
∵
| AB |
| MD |
| ||
| 2 |
| ||
| 2 |
∴cosθ=
|
| ||||
|
|
| 1 |
| 2 |
∴θ=
| π |
| 3 |
| π |
| 3 |
(3)设点B到平面OCD的距离为d,则d为
| OB |
| n |
| 2 |
由
| OB |
|
| ||||
|
| 2 |
| 3 |
所以点B到平面OCD的距离为
| 2 |
| 3 |
点评:培养学生利用多种方法解决数学问题的能力,考查学生利用空间向量求直线间的夹角和距离的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
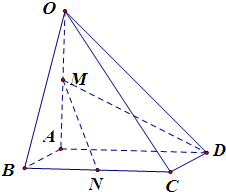 如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC中点,以A为原点,建立适当的空间直角坐标系,利用空间向量解答以下问题
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC中点,以A为原点,建立适当的空间直角坐标系,利用空间向量解答以下问题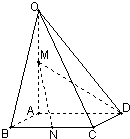 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC= 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形, 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,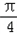 ,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.
,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.