题目内容
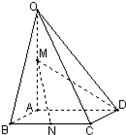
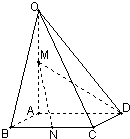
 如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC中点,以A为原点,建立适当的空间直角坐标系,利用空间向量解答以下问题
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC中点,以A为原点,建立适当的空间直角坐标系,利用空间向量解答以下问题(1)证明:直线BD⊥OC
(2)证明:直线MN∥平面OCD
(3)求异面直线AB与OC所成角的余弦值.
分析:以A为原点,以AO,AB,AD分别为x轴、y轴、z轴建立空间直角坐标系,A-xyz.
(1)要证明BD⊥OC,只要证明
•
=0即可;
(2)设平面OCD的法向量为
=(x,y,z),可得
,求出法向量
,只要证明
•
=0即可;
(3)利用cos<
,
>=
即可得出.
(1)要证明BD⊥OC,只要证明
| BD |
| OC |
(2)设平面OCD的法向量为
| n |
|
| n |
| n |
| MN |
(3)利用cos<
| AB |
| OC |
| ||||
|
|
解答:解:以A为原点,以AO,AB,AD分别为x轴、y轴、z轴建立空间直角坐标系,A-xyz.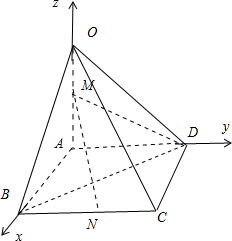
则B(1,0,0),D(0,1,0),C(1,1,0),O(0,0,2),M(0,0,1),N(1,
,0).
(1)∵
=(-1,1,0),
=(1,1,-2),
•
=-1+1+0=0,
∴
⊥
,∴BD⊥OC;
(2)
=(-1,0,0),设平面OCD的法向量为
=(x,y,z),则
,
令y=2,则x=0,z=1,∴
=(0,2,1),
又
=(1,
,-1),∴
•
=2×
-1×1=0,
而MN?平面OCD,∴MN∥平面OCD.
(3)
=(1,0,0),∴cos<
,
>=
=
=
,
∴异面直线AB与OC所成角的余弦值为
.

则B(1,0,0),D(0,1,0),C(1,1,0),O(0,0,2),M(0,0,1),N(1,
| 1 |
| 2 |
(1)∵
| BD |
| OC |
| BD |
| OC |
∴
| BD |
| OC |
(2)
| CD |
| n |
|
令y=2,则x=0,z=1,∴
| n |
又
| MN |
| 1 |
| 2 |
| n |
| MN |
| 1 |
| 2 |
而MN?平面OCD,∴MN∥平面OCD.
(3)
| AB |
| AB |
| OC |
| ||||
|
|
| 1 | ||
1×
|
| ||
| 6 |
∴异面直线AB与OC所成角的余弦值为
| ||
| 6 |
点评:熟练掌握通过建立空间直角坐标系的方法求证垂直、线面平行及求出异面直线所成的角等是解题的关键.

练习册系列答案
相关题目
 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC= 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形, 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,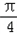 ,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.
,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.