题目内容
在某次测验中,有5位同学的平均成绩为80分,用xn表示编号为n(n=1,2,3,4,5)的同学所得成绩,且前4位同学的成绩如下:
(Ⅰ)求第5位同学的成绩x5及这5位同学成绩的标准差;
(注:标准差S=
,其中
为x1,x2…xn的平均数)
(Ⅱ)从这5位同学中,随机地选3名同学,求恰有2位同学的成绩在80(含80)分以上的概率.
| 编号n | 1 | 2 | 3 | 4 |
| 成绩xn | 81 | 79 | 80 | 78 |
(注:标准差S=
|
| . |
| x |
(Ⅱ)从这5位同学中,随机地选3名同学,求恰有2位同学的成绩在80(含80)分以上的概率.
(Ⅰ)根据题意,5个学生的平均成绩为80,则
(81+79+80+78+x5)=80
解可得x5=82,
其方差S2=
[(81-80)2+(79-80)2+(80-80)2+(80-80)2+(82-80)2]=2,
标准差S=
;
(Ⅱ)记“恰有2位同学成绩在80分以上”为事件A,
从这5名同学中随机选3名,其成绩可以为(81,79,80),(81,79,78),(81,79,82),(81,80,78),(81,80,82)(81,78,82),(79,80,78),(79,80,82),(78,78,82),(80,78,82)共10种情况,
事件A包含6种情况,
P(A)=
=
.
| 1 |
| 5 |
解可得x5=82,
其方差S2=
| 1 |
| 5 |
标准差S=
| 2 |
(Ⅱ)记“恰有2位同学成绩在80分以上”为事件A,
从这5名同学中随机选3名,其成绩可以为(81,79,80),(81,79,78),(81,79,82),(81,80,78),(81,80,82)(81,78,82),(79,80,78),(79,80,82),(78,78,82),(80,78,82)共10种情况,
事件A包含6种情况,
P(A)=
| 6 |
| 10 |
| 3 |
| 5 |

练习册系列答案
相关题目
在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 70 | 76 | 72 | 70 | 72 |
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
在某次测验中,有5位同学的平均成绩为80分,用xn表示编号为n(n=1,2,3,4,5)的同学所得成绩,且前4位同学的成绩如下:
(Ⅰ)求第5位同学的成绩x5及这5位同学成绩的标准差;
(注:标准差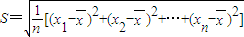 ,其中
,其中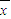 为x1,x2…xn的平均数)
为x1,x2…xn的平均数)
(Ⅱ)从这5位同学中,随机地选3名同学,求恰有2位同学的成绩在80(含80)分以上的概率.
| 编号n | 1 | 2 | 3 | 4 |
| 成绩xn | 81 | 79 | 80 | 78 |
(注:标准差
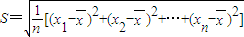 ,其中
,其中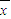 为x1,x2…xn的平均数)
为x1,x2…xn的平均数)(Ⅱ)从这5位同学中,随机地选3名同学,求恰有2位同学的成绩在80(含80)分以上的概率.