题目内容
设{an}是等差数列,数列{bn}满足bn=anan+1an+2(n∈N*),{bn}的前n项和用Sn表示,若3a5=8a12>0,试问n为多大时,Sn达到最大,并加以证明.
答案:
解析:
解析:
|
解:由3a5=8a12>0,可得a5=- 所以b16>-b15.所以S16=S14+b15+b16>S14.故n=16时,Sn达到最大. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
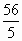 d且d<0.所以a16=-
d且d<0.所以a16=-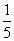 d>0,a17=
d>0,a17= d<0.从而可知b1>b2>…>b14>0>b17>b18>…,而b15=a15a16a17<0,a16=a16a17a18>0,
d<0.从而可知b1>b2>…>b14>0>b17>b18>…,而b15=a15a16a17<0,a16=a16a17a18>0,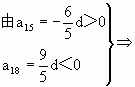 |a18|>a15.
|a18|>a15.