题目内容
 (2013•永州一模)如图所示,直角梯形ABCD中,∠A=∠D=90°,AD=2,AB=3,CD=4,P在线段AB上,BP=1,O在CD上,且OP∥AD,将图甲沿OP折叠使得平面OCBP⊥底面ADOP,得到一个多面体(如图乙),M、N分别是AC、OP的中点.
(2013•永州一模)如图所示,直角梯形ABCD中,∠A=∠D=90°,AD=2,AB=3,CD=4,P在线段AB上,BP=1,O在CD上,且OP∥AD,将图甲沿OP折叠使得平面OCBP⊥底面ADOP,得到一个多面体(如图乙),M、N分别是AC、OP的中点.(1)求证:MN⊥平面ACD;
(2)求平面ABC与底面OPAD所成角(锐角)的余弦值.
分析:(1)取CD中点Q,结合已知条件,利用线面垂直的判定定理证出OQ垂直于平面ACD,通过证明四边形OQMN为平行四边形得到OQ平行于MN,从而证出要证的结论;
(2)以O为坐标原点,分别以OP,OD,OC为x轴,y轴,z轴建立空间直角坐标系,求出平面ABC与底面OPAD的一个法向量,利用法向量所成角的余弦值得到平面ABC与底面OPAD所成角(锐角)的余弦值.
(2)以O为坐标原点,分别以OP,OD,OC为x轴,y轴,z轴建立空间直角坐标系,求出平面ABC与底面OPAD的一个法向量,利用法向量所成角的余弦值得到平面ABC与底面OPAD所成角(锐角)的余弦值.
解答:(1)证明:如图,
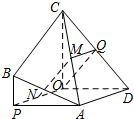 取CD的中点为Q,连接MQ,OQ,
取CD的中点为Q,连接MQ,OQ,
因为OC=OD,所以OQ⊥CD,
依题意知:面OCD⊥底面OPAD,
AD⊥OD,AD⊥平面OCD,
而OQ?面OCD,AD⊥OQ,
又CD∩AD=D,
所以OQ⊥面ACD,
MQ是△ACD的中位线,故MQ∥
AD,MQ=
AD,
NO∥
AD,NO=
AD,
则MQNO,所以MN∥OQ,
故MN⊥平面ACD;
(2)解:如图所示,分别以OP,OD,OC为x轴,y轴,z轴建立空间直角坐标系.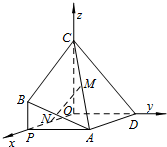
B(2,0,1),A(2,2,0)C(0,0,2),
底面OPAD的一个法向量
=(0,0,1),
设平面ABC的法向量为
=(x,y,z),
=(0,-2,1),
=(2,0,-1),
依题知:
,
即
,
令x=1,则y=1,z=2,
=(1,1,2),
所以 cos<
,
>=
=
,
故平面ABC与底面OPAD所成角的余弦值为
.
 取CD的中点为Q,连接MQ,OQ,
取CD的中点为Q,连接MQ,OQ,因为OC=OD,所以OQ⊥CD,
依题意知:面OCD⊥底面OPAD,
AD⊥OD,AD⊥平面OCD,
而OQ?面OCD,AD⊥OQ,
又CD∩AD=D,
所以OQ⊥面ACD,
MQ是△ACD的中位线,故MQ∥
| 1 |
| 2 |
| 1 |
| 2 |
NO∥
| 1 |
| 2 |
| 1 |
| 2 |
则MQNO,所以MN∥OQ,
故MN⊥平面ACD;
(2)解:如图所示,分别以OP,OD,OC为x轴,y轴,z轴建立空间直角坐标系.

B(2,0,1),A(2,2,0)C(0,0,2),
底面OPAD的一个法向量
| m |
设平面ABC的法向量为
| n |
| AB |
| CB |
依题知:
|
即
|
令x=1,则y=1,z=2,
| n |
所以 cos<
| m |
| n |
| 2 | ||
1×
|
| ||
| 3 |
故平面ABC与底面OPAD所成角的余弦值为
| ||
| 3 |
点评:本题考查了直线与平面垂直的判定,考查了二面角的平面角及其求法,综合考查了学生的空间想象能力和思维能力,解答的关键是明确折叠问题在折叠前后的变量和不变量,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目