题目内容
椭圆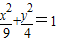 的焦点F1、F2,点P为其上的动点,当∠F1PF2为钝角时,点P横坐标的取值范围是______
的焦点F1、F2,点P为其上的动点,当∠F1PF2为钝角时,点P横坐标的取值范围是______
【答案】分析:设p(x,y),根据椭圆方程求得两焦点坐标,根据∠F1PF2是钝角推断出PF21+PF22<F1F22代入p坐标求得x和y的不等式关系,求得x的范围.
解答:解:设p(x,y),则F1(-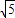 ,0),F2(
,0),F2(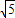 ,0),
,0),
∵∠F1PF2是钝角,∴cos∠F1PF2=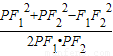 <0,
<0,
∴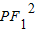 +
+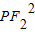 <
<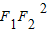 ,
,
∴(x+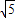 )2+y2+(x-
)2+y2+(x-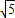 )2+y2<20,
)2+y2<20,
∴x2+5+y2<10,
∴x2+4(1- )<5,
)<5,
∴x2< ,解得-
,解得- <x<
<x<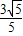 .
.
故答案为:(-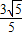 ,
,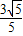 ).
).
点评:本题主要考查了椭圆的简单性质和解不等式,∠F1PF2是钝角推断出PF21+PF22<F1F22,是解题关键,属中档题.
解答:解:设p(x,y),则F1(-
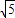 ,0),F2(
,0),F2(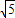 ,0),
,0),∵∠F1PF2是钝角,∴cos∠F1PF2=
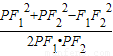 <0,
<0,∴
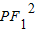 +
+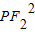 <
<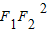 ,
,∴(x+
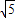 )2+y2+(x-
)2+y2+(x-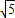 )2+y2<20,
)2+y2<20,∴x2+5+y2<10,
∴x2+4(1-
 )<5,
)<5,∴x2<
 ,解得-
,解得- <x<
<x<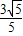 .
.故答案为:(-
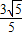 ,
,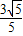 ).
).点评:本题主要考查了椭圆的简单性质和解不等式,∠F1PF2是钝角推断出PF21+PF22<F1F22,是解题关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
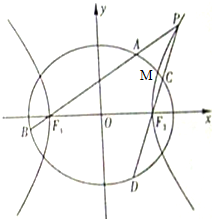 (2011•天津模拟)如图,椭圆
(2011•天津模拟)如图,椭圆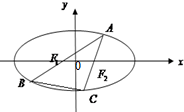 椭圆
椭圆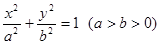 的焦点F1,F2,短轴长为8,离心率为
的焦点F1,F2,短轴长为8,离心率为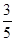 ,过F1的直线交椭圆于A、B两点,则
,过F1的直线交椭圆于A、B两点,则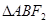 的周长为( )
的周长为( )