题目内容

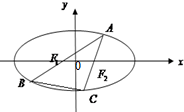精英家教网椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的内接三角形ABC（顶点A、B、C都在椭圆上）的边AB，AC分别过椭圆的焦点F1和F2，则△ABC的周长（　　）
分析：由椭圆的定义可得AF1+AF2=2a，BF1+BF2=2a，CF1+CF2=2a，三式相加可得AF1+AF2+BF1+BF2+CF1+CF2=6a，结合△ABC周长，即可得出结论．
解答：解：连接BF2，CF1，则AF1+AF2=2a，BF1+BF2=2a，CF1+CF2=2a，
三式相加可得AF1+AF2+BF1+BF2+CF1+CF2=6a
∴AB+AC+BF2+CF1=6a，
∵BF2+CF1＞BC，
∴AB+AC+BC＜6a
故选C．
点评：本题考查三角形的周长，考查椭圆的定义，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
已知椭圆
x2
a2
+
y2
b
=1(a＞b＞0)的左、右焦点分别为F1、F2，离心率e=
2
2
，右准线方程为x=2．
（1）求椭圆的标准方程；
（2）过点F1的直线l与该椭圆交于M、N两点，且|
F2M
+
F2N
|=
2
26
3
，求直线l的方程．
精英家教网如图，椭圆
x2
a2
+
y2
b 
=1（a＞b＞0）与过点A（2，0）B（0，1）的直线有且只有一个公共点T，且椭圆的离心率e=
3
2
．
（Ⅰ）求椭圆方程；
（Ⅱ）设F1、F2分别为椭圆的左、右焦点，求证：|AT|2=
1
2
|AF1||AF2|．
精英家教网如图，椭圆
x2
a2
+
y2
b 
=1（a＞b＞0）与过点A（2，0）B（0，1）的直线有且只有一个公共点T，且椭圆的离心率e=
3
2
．
（Ⅰ）求椭圆方程；
（Ⅱ）设F1、F2分别为椭圆的左、右焦点，M为线段AF1的中点，求证：∠ATM=∠AF1T．
设 A（x1，y1）、B（x2，y2）是椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）上的两点，O为坐标原点，向量
m
=(
x1
a
，
y1
b
)，
n
=(
x2
a
，
y2
b
)且
m
•
n
=0．
（1）若A点坐标为（a，0），求点B的坐标；
（2）设
OM
=cosθ•
OA
+sinθ•
OB
，证明点M在椭圆上；
（3）若点P、Q为椭圆 上的两点，且
PQ
∥
OB
，试问：线段PQ能否被直线OA平分？若能平分，请加以证明；若不能平分，请说明理由．
已知椭圆
x2
a2
+
y2
b
=1(a＞b＞0)的左、右焦点分别为F1、F2，离心率e=
2
2
，右准线方程为x=2．
（1）求椭圆的标准方程；
（2）过点F1的直线l与该椭圆交于M、N两点，且|
F2M
+
F2N
|=
2
26
3
，求直线l的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网