题目内容

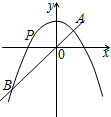
曲线y=x2与直线x+y=2围成的图形的面积为（　　）
A．
7
2
B．4C．
9
2
D．5
解先根据题意画出图形，得到积分上限为1，积分下限为-2
曲线y=x2与直线x+y=2围成的图形的面积为：
S=∫-21（2-x-x2）dx
而∫-21（2-x-x2）dx=（2x-
1
2
x2-
1
3
x3）|-21=
9
2

∴曲边梯形的面积是
9
2

故选C．
练习册系列答案
相关题目
如图，ABCD是边长为l的正方形，O为AD的中点，抛物线的顶点为O，且通过点C，则阴影部分的面积为（　　）
A．
1
4
B．
1
2
C．
1
3
D．
3
4
如图，已知抛物线y=4-x2与直线y=3x的两个交点分别为A、B，点P在抛物线上从A向B运动（点P不同于点A、B），
（Ⅰ）求由抛物线y=4-x2与直线y=3x所围成的图形面积；
（Ⅱ）求使△PAB的面积为最大时P点的坐标．
设f(x)=
sinx，x∈[0，
π
2
)
1，x∈[
π
2
，2]
，则
∫20
f(x)dx为______．
曲线y=x2和曲线y=
x
围成一个叶形图（如图所示阴影部分），其面积是______．
由曲线xy=1，直线y=x，y=4所围成的平面图形的面积为（　　）
A．
32
9
B．8-ln2C．
15
2
-2ln2		D．8-2ln2
过抛物线y=x2上一动点P（t，t2）（0＜t＜1）作此抛物线的切线l，抛物线y=x2与直线x=0、x=1及切线l围成的图形的面积为S，则S的最小值为（　　）
A．
1
12
B．
1
10
C．
1
6
D．
1
4
已知曲线f（x）=x2．
（1）求曲线f（x）在（1，1）点处的切线l的方程；
（2）求由曲线f（x）、直线x=0和直线l所围成图形的面积．
函数的定义域为  
A．
B．为第Ⅰ、Ⅱ象限的角
C．
D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网