题目内容
(2013•丰台区一模)已知a∈Z,关于x的一元二次不等式x2-6x+a≤0的解集中有且仅有3个整数,则所有符合条件的a的值之和是( )
分析:设f(x)=x2-6x+a,其图象是开口向上,对称轴是x=3的抛物线,如图所示.利用数形结合的方法得出,若关于x的一元二次不等式x2-6x+a≤0的解集中有且仅有3个整数,则
,从而解出所有符合条件的a的值之和.
|
解答: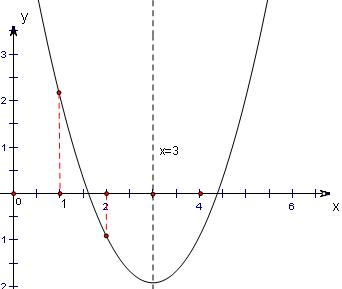 解:设f(x)=x2-6x+a,其图象是开口向上,对称轴是x=3的抛物线,如图所示.
解:设f(x)=x2-6x+a,其图象是开口向上,对称轴是x=3的抛物线,如图所示.
若关于x的一元二次不等式x2-6x+a≤0的解集中有且仅有3个整数,则
,即
,
解得5<a≤8,又a∈Z,∴a=6,7,8.
则所有符合条件的a的值之和是6+7+8=21.
故选C.
 解:设f(x)=x2-6x+a,其图象是开口向上,对称轴是x=3的抛物线,如图所示.
解:设f(x)=x2-6x+a,其图象是开口向上,对称轴是x=3的抛物线,如图所示.若关于x的一元二次不等式x2-6x+a≤0的解集中有且仅有3个整数,则
|
|
解得5<a≤8,又a∈Z,∴a=6,7,8.
则所有符合条件的a的值之和是6+7+8=21.
故选C.
点评:本题主要考查一元二次不等式,以及根的存在性及根的个数判断问题,同时考查了转化的思想,属于中档题.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 (2013•丰台区一模)执行右边的程序框图所得的结果是( )
(2013•丰台区一模)执行右边的程序框图所得的结果是( )