题目内容
已知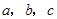 为
为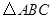 的三个内角
的三个内角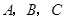 的对边,向量
的对边,向量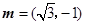 ,
,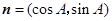 .若
.若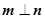 ,且
,且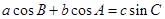 ,则角
,则角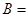 ( )
( )
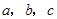 为
为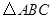 的三个内角
的三个内角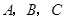 的对边,向量
的对边,向量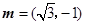 ,
,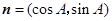 .若
.若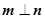 ,且
,且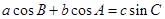 ,则角
,则角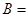 ( )
( )A. | B. | C. | D. |
C
由向量数量积的意义,有 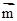 ⊥
⊥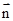 ?
?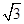 cosA-sinA=0,进而可得A,再根据正弦定理,可得,结合和差公式的正弦形式,
cosA-sinA=0,进而可得A,再根据正弦定理,可得,结合和差公式的正弦形式,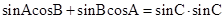 化简可得sinC=sin2C,可得C,由A、C的大小可得答案
化简可得sinC=sin2C,可得C,由A、C的大小可得答案
根据题意,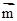 ⊥
⊥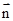 ?
?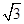 cosA-sinA=0
cosA-sinA=0
?A=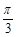 ,由正弦定理可得,
,由正弦定理可得,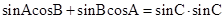 ,
,
又由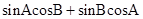 =sin(A+B)=sinC,
=sin(A+B)=sinC,
化简可得,sinC=sin2C,则C=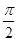 ,则B=
,则B=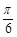 ,
,
故答案为C
本题考查向量数量积的应用,判断向量的垂直,解题时,注意向量的正确表示方法
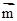 ⊥
⊥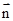 ?
?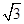 cosA-sinA=0,进而可得A,再根据正弦定理,可得,结合和差公式的正弦形式,
cosA-sinA=0,进而可得A,再根据正弦定理,可得,结合和差公式的正弦形式,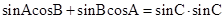 化简可得sinC=sin2C,可得C,由A、C的大小可得答案
化简可得sinC=sin2C,可得C,由A、C的大小可得答案根据题意,
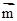 ⊥
⊥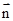 ?
?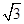 cosA-sinA=0
cosA-sinA=0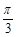 ,由正弦定理可得,
,由正弦定理可得,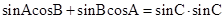 ,
,又由
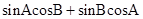 =sin(A+B)=sinC,
=sin(A+B)=sinC,化简可得,sinC=sin2C,则C=
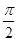 ,则B=
,则B=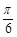 ,
,故答案为C
本题考查向量数量积的应用,判断向量的垂直,解题时,注意向量的正确表示方法

练习册系列答案
相关题目
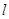 的方向向量
的方向向量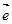 =(
=(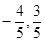 ),点
),点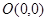 和
和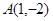 在
在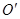 和
和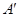 ,则
,则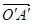 =
=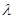
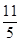
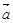 =(-2,1),
=(-2,1),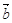 =(λ,-1),若
=(λ,-1),若



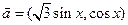 ,
,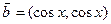 .
. 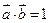 ,且
,且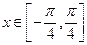 ,求
,求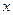 的值;
的值; 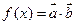 ,求
,求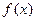 的周期及单调减区间.
的周期及单调减区间.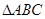 中,已知
中,已知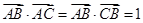 ,则
,则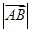 的值为 ( )
的值为 ( )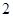
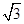
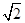
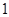
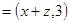 ,b
,b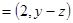 ,且a⊥b.若
,且a⊥b.若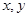 满足不等式
满足不等式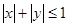 ,则
,则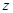 的取值范围 .
的取值范围 .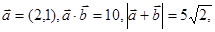 则
则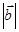 等于( )
等于( )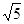
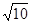
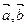 是两个非零向量,且
是两个非零向量,且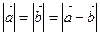 ,则
,则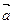 与
与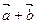 的夹角大小为_________
的夹角大小为_________