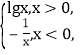题目内容
【题目】红队队员甲、乙、丙与蓝队队员A、B、C进行围棋比赛，甲对A，乙对B，丙对C各一盘，已知甲胜A，乙胜B，丙胜C的概率分别为
，
，，假设各盘比赛结果相互独立．
（I）求红队至少两名队员获胜的概率；
（II）用
表示红队队员获胜的总盘数，求的分布列和数学期望
．
【答案】（Ⅰ）
；（Ⅱ）详见解析
【解析】
解：（I）设甲胜A的事件为D，乙胜B的事件为E，丙胜C的事件为F，
则
分别表示甲不胜A、乙不胜B，丙不胜C的事件．
因为
，
．
红队至少两人获胜的事件有：
，
由于以上四个事件两两互斥且各盘比赛的结果相互独立，因此红队至少两人获胜的概率
（II）由题意知
可能的取值为0，1，2，3．
又由（I）知
是两两互斥事件，且各盘比赛的结果相互独立，
因此
，
，
由对立事件的概率公式得
所以的分布列为：
|
|
|
|
|
|
|
|
|
|
因此
练习册系列答案
相关题目
【题目】某人在如图所示的直角边长为4米的三角形地块的每个格点（指纵、横直线的交叉点以及三角形的顶点）处都种了一株相同品种的作物．根据历年的种植经验，一株该种作物的年收货量
(单位：kg)与它的“相近”作物株数
之间的关系如下表所示：
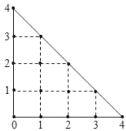
X | 1 | 2 | 3 | 4 |
Y | 51 | 48 | 45 | 42 |
这里，两株作物“相近”是指它们之间的直线距离不超过1米．
（Ⅰ）完成下表,并求所种作物的平均年收获量;
Y | 51 | 48 | 45 | 42 |
频数 | 4 |
(Ⅱ)在所种作物中随机选取一株,求它的年收获量至少为48kg的概率.
