题目内容
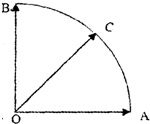
给定两个长度为1的平面向量
和
,它们的夹角为90°,如图所示,点C在以O为圆心的圆弧AB上运动,若
=x
+y
,其中x,y∈R,则x+y的最大值是( )
| OA |
| OB |
| CO |
| OA |
| OB |
| A.1 | B.
| C.
| D.2 |

∵点C在以O为圆心的圆弧AB上运动,
∴可以设圆的参数方程x=cosθ,y=sinθ,θ∈[0°,90°]
∴x+y=cosθ+sinθ=
sin(θ+
)
∵θ∈[0°,90°]
∴θ+
∈[45°,135°],
∴x+y的最大值是
,当三角函数取到1时成立.
故选B.
∴可以设圆的参数方程x=cosθ,y=sinθ,θ∈[0°,90°]
∴x+y=cosθ+sinθ=
| 2 |
| π |
| 4 |
∵θ∈[0°,90°]
∴θ+
| π |
| 4 |
∴x+y的最大值是
| 2 |
故选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的参数方程为
的参数方程为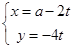 ,(
,( 为参数),圆
为参数),圆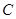 的参数方程为
的参数方程为 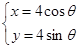 ,(
,(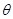 为参数).
为参数).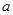 的取值范围.
的取值范围.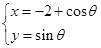 (θ为参数,θ∈R)上,则
(θ为参数,θ∈R)上,则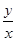 的取值范围是 .
的取值范围是 .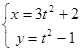 (t是参数),则曲线是( )
(t是参数),则曲线是( )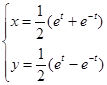 中当
中当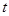 为参数时,化为普通方程为_______________.
为参数时,化为普通方程为_______________.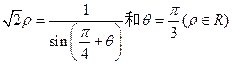 ,则两直线交点的极坐标为 .
,则两直线交点的极坐标为 .